2. Add Two Numbers

Problem:

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Example

Input: (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 0 -> 8
Explanation: 342 + 465 = 807.

Solution:

Mind the last carry.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
let addTwoNumbers = function(l1, l2) {
  const prehead = new ListNode()
  let p = prehead
  let carry = 0

  for (let p1 = l1, p2 = l2: p1 || p2 || carry > 0; p = p.next) {
    let sum = carry
    if (p1) {
      sum += p1.val
      p1 = p1.next
    }
    if (p2) {
      sum += p2.val
      p2 = p2.next
    }
    carry = sum / 10 | 0
    p.next = new ListNode(sum % 10)
  }

  return prehead.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Binary Search”: https://leetcode.com/tag/binary-search “Divide and Conquer”: https://leetcode.com/tag/divide-and-conquer

4. Median of Two Sorted Arrays

Problem:

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

Solution:

O(log (m+n)) means half of the sequence is ruled out on each loop. So obviously we need binary search.

To do it on two sorted arrays, we need a formula to guide division.

Let nums3 be the sorted array combining all the items in nums1 and nums2.

If nums2[j-1] <= nums1[i] <= nums2[j], then we know nums1[i] is at num3[i+j]. Same goes nums1[i-1] <= nums2[j] <= nums1[i].

Let k be ⌊(m+n-1)/2⌋. We need to find nums3[k] (and also nums3[k+1] if m+n is even).

Let i + j = k, if we find nums2[j-1] <= nums1[i] <= nums2[j] or nums1[i-1] <= nums2[j] <= nums1[i], then we got k.

Otherwise, if nums1[i] <= nums2[j] then we know nums1[i] < nums2[j-1] (because we did not find k).

• There are i items before nums1[i], and j-1 items brefor nums2[j-1], which means nums1[0...i] are before nums3[i+j-1]. So we now know nums1[0...i] < nums3[k]. They can be safely discarded.

• We Also have nums1[i] < nums2[j], which means nums2[j...n) are after nums3[i+j]. So nums2[j...n) > nums3[k].

Same goes nums1[i-1] <= nums2[j] <= nums1[i].

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
let findMedianSortedArrays = function (nums1, nums2) {
  const mid = (nums1.length + nums2.length - 1) / 2 | 0

  if ((nums1.length + nums2.length) % 2 === 0) {
    return (_find(nums1, nums2, mid) + _find(nums1, nums2, mid + 1)) / 2
  }

  return _find(nums1, nums2, mid)
}


function _find (nums1, nums2, k) {
  if (nums1.length > nums2.length) {
    // So that the `i` below is always smalller than k,
    // which makes `j` always non-negative
    [nums1, nums2] = [nums2, nums1]
  }
  let s1 = 0
  let s2 = 0
  let e1 = nums1.length
  let e2 = nums2.length

  while (s1 < e1 || s2 < e2) {
    const i = s1 + ((e1 - s1) / 2 | 0)
    const j = k - i
    const ni = i >= e1 ? Infinity : nums1[i]
    const nj = j >= e2 ? Infinity : nums2[j]
    const ni_1 = i <= 0 ? -Infinity : nums1[i-1]
    const nj_1 = j <= 0 ? -Infinity : nums2[j-1]

    if (nj_1 <= ni && ni <= nj) {
      return ni
    }

    if (ni_1 <= nj && nj <= ni) {
      return nj
    }

    if (ni <= nj) {
      s1 = i + 1
      e2 = j
    } else {
      s2 = j + 1
      e1 = i
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “String”: https://leetcode.com/tag/string

6. ZigZag Conversion

Problem:

The string "PAYPALISHIRING" is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)

P   A   H   N
A P L S I I G
Y   I   R

And then read line by line: "PAHNAPLSIIGYIR"

Write the code that will take a string and make this conversion given a number of rows:

string convert(string s, int numRows);

Example 1:

Input: s = "PAYPALISHIRING", numRows = 3
Output: "PAHNAPLSIIGYIR"

Example 2:

Input: s = "PAYPALISHIRING", numRows = 4
Output: "PINALSIGYAHRPI"
Explanation:

P     I    N
A   L S  I G
Y A   H R
P     I

Solution:

Squeeze the zigzag pattern horizontally to form a matrix. Now deal with the odd and even columns respectively.

For example let numRows be 5, if we list out the indecies:

row
 1    00    08    16
 2    01 07 09 15 17
 3    02 06 10 14 18
 4    03 05 11 13 19
 5    04    12    20

First calculate the matrix width:

pairs = floor( len(s) / (numRows + numRows - 2) )
width = pairs * 2 + ceil( (len(s) - pairs * (numRows + numRows - 2)) / numRows )

We can easily make a observation that the direction of odd and even columns and different.

Let the first column be index 0 and let i be the current position at column col.

We need to count the items between matrix[row][col] and matrix[row][col+1], exclusive.

next_i = i + (numRows - row) + (numRows - row), if col is even && 1 < row < numRows
next_i = i + row - 2 + row, if col is odd && 1 < row < numRows

If row == 1 or row == numRows, skip the odd columns.

next_i = i + numRows + (numRows - 2), if col is even && (row == 1 || row == numRows)

/**
 * @param {string} s
 * @param {number} numRows
 * @return {string}
 */
let convert = function(s, numRows) {
  if (numRows <= 1) { return s }

  const pairs = Math.floor(s.length / (numRows + numRows - 2))
  const width = pairs * 2 + Math.ceil((s.length - pairs * (numRows + numRows - 2)) / numRows)

  let result = ''

  for (let row = 1; row <= numRows; row++) {
    let i = row - 1
    result += s[i] || ''
    for (let col = 0; col < width; col++) {
      if (row === 1 || row === numRows) {
        if (col % 2 === 0) {
          i += numRows + (numRows - 2)
        } else {
          continue
        }
      } else {
        if (col % 2 === 0) {
          i += (numRows - row) + (numRows - row)
        } else {
          i += row - 2 + row
        }
      }
      result += s[i] || ''
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Math”: https://leetcode.com/tag/math Similar Questions: “String to Integer (atoi)”: https://leetcode.com/problems/string-to-integer-atoi

7. Reverse Integer

Problem:

Given a 32-bit signed integer, reverse digits of an integer.

Example 1:

Input: 123
Output: 321

Example 2:

Input: -123
Output: -321

Example 3:

Input: 120
Output: 21

Note:
Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−231,  231 − 1]. For the purpose of this problem, assume that your function returns 0 when the reversed integer overflows.

Solution:

ONE

This is a JavaScript specific solution. It is esay to write but slow to run because it generates O(n) space. This could end up a huge array.

/**
 * @param {number} x
 * @return {number}
 */
let reverse = function(x) {
  let n = Math.abs(x).toString().split('').reverse().join('')
  if (n > 2147483647) { return 0 }
  return (x < 0? -1: 1) * n
};

TWO

Pure mathamatical solution.

/**
 * @param {number} x
 * @return {number}
 */
let reverse = function(x) {
  let result = 0
  while (x) {
    result = result * 10 + x % 10
    x = x / 10 | 0
  }
  return Math.abs(result) > 2147483647 ? 0 : result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Math”: https://leetcode.com/tag/math “String”: https://leetcode.com/tag/string Similar Questions: “Reverse Integer”: https://leetcode.com/problems/reverse-integer “Valid Number”: https://leetcode.com/problems/valid-number

8. String to Integer (atoi)

Problem:

Implement atoi which converts a string to an integer.

The function first discards as many whitespace characters as necessary until the first non-whitespace character is found. Then, starting from this character, takes an optional initial plus or minus sign followed by as many numerical digits as possible, and interprets them as a numerical value.

The string can contain additional characters after those that form the integral number, which are ignored and have no effect on the behavior of this function.

If the first sequence of non-whitespace characters in str is not a valid integral number, or if no such sequence exists because either str is empty or it contains only whitespace characters, no conversion is performed.

If no valid conversion could be performed, a zero value is returned.

Note:

Only the space character ' ' is considered as whitespace character.
Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−231,  231 − 1]. If the numerical value is out of the range of representable values, INT_MAX (231 − 1) or INT_MIN (−231) is returned.

Example 1:

Input: "42"
Output: 42

Example 2:

Input: "   -42"
Output: -42
Explanation: The first non-whitespace character is '-', which is the minus sign.
             Then take as many numerical digits as possible, which gets 42.

Example 3:

Input: "4193 with words"
Output: 4193
Explanation: Conversion stops at digit '3' as the next character is not a numerical digit.

Example 4:

Input: "words and 987"
Output: 0
Explanation: The first non-whitespace character is 'w', which is not a numerical
             digit or a +/- sign. Therefore no valid conversion could be performed.

Example 5:

Input: "-91283472332"
Output: -2147483648
Explanation: The number "-91283472332" is out of the range of a 32-bit signed integer.
             Thefore INT_MIN (−231) is returned.

Solution:

ONE

/**
 * @param {string} str
 * @return {number}
 */
let myAtoi = function (str) {
  return Math.min(2147483647, Math.max(-2147483648, parseInt(str))) || 0
};

TWO

Looks like Number() is faster than parseInt().

/**
 * @param {string} str
 * @return {number}
 */
let myAtoi = function (str) {
  return Math.min(2147483647, Math.max(-2147483648, (/^ *[-+]?\d+/.exec(str) || [0])[0]))
};

THREE

General solution.

/**
 * @param {string} str
 * @return {number}
 */
let myAtoi = function (str) {
  let sign = 1
  let i = 0

  while (i < str.length) {
    const cc = str.charCodeAt(i++)
    if (cc === 45) { // -
      sign = -1
      break
    } else if (cc === 43) { // +
      break
    } else if (cc >= 48 && cc <= 57) { // 0-9
      i--
      break
    } else if (cc !== 32) { // space
      return 0
    }
  }

  let result = 0
  while (i < str.length) {
    const digit = str.charCodeAt(i++) - 48
    if (digit < 0 || digit > 9) {
      break
    }
    result = result * 10 + digit
  }

  return Math.min(2147483647, Math.max(-2147483648, result * sign))
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Math”: https://leetcode.com/tag/math Similar Questions: “Palindrome Linked List”: https://leetcode.com/problems/palindrome-linked-list

9. Palindrome Number

Problem:

Determine whether an integer is a palindrome. An integer is a palindrome when it reads the same backward as forward.

Example 1:

Input: 121
Output: true

Example 2:

Input: -121
Output: false
Explanation: From left to right, it reads -121. From right to left, it becomes 121-. Therefore it is not a palindrome.

Example 3:

Input: 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome.

Follow up:

Coud you solve it without converting the integer to a string?

Solution:

ONE

Easy to write but slow since it generates an array.

/**
 * @param {number} x
 * @return {boolean}
 */
let isPalindrome = function(x) {
  return x == String(x).split('').reverse().join('')
};

TWO

A bit faster.

/**
 * @param {number} x
 * @return {boolean}
 */
let isPalindrome = function(x) {
  const s = String(x)
  for (let i = 0, j = s.length -1; i < j; i++, j--) {
    if (s[i] !== s[j]) {
      return false
    }
  }
  return true
};

THREE

General solution. Combining 7. Reverse Integer.

/**
 * @param {number} x
 * @return {boolean}
 */
let isPalindrome = function(x) {
  if (x < 0) { return false }
  return x === reverse(x)
};

/**
 * @param {number} x
 * @return {number}
 */
function reverse (x) {
  let result = 0
  while (x) {
    result = result * 10 + x % 10
    x = x / 10 | 0
  }
  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “String”: https://leetcode.com/tag/string “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Wildcard Matching”: https://leetcode.com/problems/wildcard-matching

10. Regular Expression Matching

Problem:

Given an input string (s) and a pattern (p), implement regular expression matching with support for '.' and '*'.

'.' Matches any single character.
'*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Note:

s could be empty and contains only lowercase letters a-z.
p could be empty and contains only lowercase letters a-z, and characters like . or *.

Example 1:

Input:
s = "aa"
p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".

Example 2:

Input:
s = "aa"
p = "a*"
Output: true
Explanation: '*' means zero or more of the precedeng element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".

Example 3:

Input:
s = "ab"
p = ".*"
Output: true
Explanation: ".*" means "zero or more (*) of any character (.)".

Example 4:

Input:
s = "aab"
p = "c*a*b"
Output: true
Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore it matches "aab".

Example 5:

Input:
s = "mississippi"
p = "mis*is*p*."
Output: false

Solution:

ONE

Cheating with real RegExp matching.

/**
 * @param {string} s
 * @param {string} p
 * @return {boolean}
 */
let isMatch = function(s, p) {
  if (p[0] === '*') { return false }
  return new RegExp(`^${p}$`).test(s)
};

TWO

Let f(i, j) be the matching result of s[0…i) and p[0…j).

f(0, j) =
    j == 0 || // empty
    p[j-1] == '*' && f(i, j-2) // matches 0 time, which matches empty string

f(i, 0) = false // pattern must cover the entire input string

f(i, j) =
    if p[j-1] == '.'
        f(i-1, j-1)
    else if p[j-1] == '*'
        f(i, j-2) || // matches 0 time
        f(i-1, j) && (s[i-1] == p[j-2] || p[j-2] == '.') // matches 1 or multiple times
    else
        f(i-1, j-1) && s[i-1] == p[j-1]

/**
 * @param {string} s
 * @param {string} p
 * @return {boolean}
 */
let isMatch = function(s, p) {
  if (p[0] === '*') {
    return false
  }

  const dp = [[true]]

  for (let j = 2; j <= p.length; j++) {
    dp[0][j] = p[j-1] === '*' && dp[0][j-2]
  }

  for (let i = 1; i <= s.length; i++) {
    dp[i] = []
    for (let j = 1; j <= p.length; j++) {
      switch (p[j-1]) {
        case '.':
          dp[i][j] = dp[i-1][j-1]
          break
        case '*':
          dp[i][j] = dp[i][j-2] ||
            dp[i-1][j] && (p[j-2] === '.' || s[i-1] === p[j-2])
          break
        default:
          dp[i][j] = dp[i-1][j-1] && s[i-1] === p[j-1]
      }
    }
  }

  return !!dp[s.length][p.length]
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Trapping Rain Water”: https://leetcode.com/problems/trapping-rain-water

11. Container With Most Water

Problem:

Given n non-negative integers a1, a2, …, an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

Solution:

Greedy Algorithm.

If we look at the simple brute force approach, where we choose one point at a time and calculate all the possible areas with other points on the right, it is easy to make a observation that we are narrowing down the horizontal distance.

Greedy Algorithm can help us skip some of the conditions. It is base on a fact that the area between two columns are determined by the shorter one.

Let’s say we have pointer l and r at the begin and end of a distance, and the area is area(l, r), how should we narrow down the distance?

If height[l] < height[r], we know that the height of the area will never be greater than height[l] if we keep l. Now if we get rid of r, the area can only get smaller since the distance is shorter, and the height is at most height[l].

Here we conclude rule NO.1: Get rid of the smaller one.

What if height[l] == height[r]? It is safe to get rid of both. We do not need any of them to constrain the max height of the rest points.

/**
 * @param {number[]} height
 * @return {number}
 */
let maxArea = function (height) {
  let max = 0
  for (let l = 0, r = height.length - 1; l < r; l++, r--) {
    max = Math.max(max, (r - l) * Math.min(height[l], height[r]))
    if (height[l] < height[r]) {
      r++
    } else {
      l--
    }
  }
  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Math”: https://leetcode.com/tag/math “String”: https://leetcode.com/tag/string Similar Questions: “Roman to Integer”: https://leetcode.com/problems/roman-to-integer “Integer to English Words”: https://leetcode.com/problems/integer-to-english-words

12. Integer to Roman

Problem:

Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.

Symbol       Value
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as, XII, which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.

Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:

• I can be placed before V (5) and X (10) to make 4 and 9.
• X can be placed before L (50) and C (100) to make 40 and 90.
• C can be placed before D (500) and M (1000) to make 400 and 900.

Given an integer, convert it to a roman numeral. Input is guaranteed to be within the range from 1 to 3999.

Example 1:

Input: 3
Output: "III"

Example 2:

Input: 4
Output: "IV"

Example 3:

Input: 9
Output: "IX"

Example 4:

Input: 58
Output: "LVIII"
Explanation: C = 100, L = 50, XXX = 30 and III = 3.

Example 5:

Input: 1994
Output: "MCMXCIV"
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.

Solution:

Treat 4, 40, 400 and 9, 90, 900 specially.

/**
 * @param {number} num
 * @return {string}
 */
let intToRoman = function(num) {
  const e = [1000, 900,  500, 400,  100, 90,   50,  40,   10,  9,    5,   4,    1  ]
  const s = ["M",  "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"]

  let result = ''
  for (let i = 0; num; i++) {
    const d = e[i]
    const v = s[i]
    while (num >= d) {
      num -= d
      result += v
    }
  }
  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Math”: https://leetcode.com/tag/math “String”: https://leetcode.com/tag/string Similar Questions: “Integer to Roman”: https://leetcode.com/problems/integer-to-roman

13. Roman to Integer

Problem:

Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.

Symbol       Value
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as, XII, which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.

Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:

• I can be placed before V (5) and X (10) to make 4 and 9.
• X can be placed before L (50) and C (100) to make 40 and 90.
• C can be placed before D (500) and M (1000) to make 400 and 900.

Given a roman numeral, convert it to an integer. Input is guaranteed to be within the range from 1 to 3999.

Example 1:

Input: "III"
Output: 3

Example 2:

Input: "IV"
Output: 4

Example 3:

Input: "IX"
Output: 9

Example 4:

Input: "LVIII"
Output: 58
Explanation: C = 100, L = 50, XXX = 30 and III = 3.

Example 5:

Input: "MCMXCIV"
Output: 1994
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.

Solution:

Normally we just add up the digits, except when the digit is greater than its left (e.g. IV). In that case we need to fallback and remove the last digit then combine the two as new digit. That is why we subtract the last digit twice.

/**
 * @param {string} s
 * @return {number}
 */
let romanToInt = function (s) {
  const rdigit = {
    I: 1,
    V: 5,
    X: 10,
    L: 50,
    C: 100,
    D: 500,
    M: 1000,
  }

  let result = 0
  for (let i = 0, lastDigit = Infinity; i < s.length; i++) {
    let digit = rdigit[s[i]]
    result += digit <= lastDigit ? digit : digit - lastDigit * 2
    lastDigit = digit
  }
  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “String”: https://leetcode.com/tag/string

14. Longest Common Prefix

Problem:

Write a function to find the longest common prefix string amongst an array of strings.

If there is no common prefix, return an empty string "".

Example 1:

Input: ["flower","flow","flight"]
Output: "fl"

Example 2:

Input: ["dog","racecar","car"]
Output: ""
Explanation: There is no common prefix among the input strings.

Note:

All given inputs are in lowercase letters a-z.

Solution:

ONE

JavaScript specific solution. Get the min len then narrow down the prefix.

/**
 * @param {string[]} strs
 * @return {string}
 */
let longestCommonPrefix = function (strs) {
  if (strs.length > 0) {
    let minLen = Math.min(...strs.map(s => s.length))
    const anyStr = strs[0]
    while (minLen) {
      const prefix = anyStr.slice(0, minLen--)
      if (strs.every(s => s.startsWith(prefix))) {
        return prefix
      }
    }
  }
  return ''
};

TWO

/**
 * @param {string[]} strs
 * @return {string}
 */
let longestCommonPrefix = function(strs) {
  if (strs.length <= 0) { return '' }

  let i = 0
  while (strs.every(s => s[i] && s[i] === strs[0][i])) {
    i++
  }
  return strs[0].slice(0, i)
};

THREE

General solution. Build up the prefix.

/**
 * @param {string[]} strs
 * @return {string}
 */
let longestCommonPrefix = function (strs) {
  let prefix = ''
  if (strs.length > 0) {
    for (let i = 0; ; i++) {
      const c = strs[0][i]
      if (!c) { return prefix }
      for (let j = 0; j < strs.length; j++) {
        if (strs[j][i] !== c) {
          return prefix
        }
      }
      prefix += c
    }
  }
  return prefix
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Two Sum”: https://leetcode.com/problems/two-sum “3Sum Closest”: https://leetcode.com/problems/3sum-closest “4Sum”: https://leetcode.com/problems/4sum “3Sum Smaller”: https://leetcode.com/problems/3sum-smaller

15. 3Sum

Problem:

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note:

The solution set must not contain duplicate triplets.

Example:

Given array nums = [-1, 0, 1, 2, -1, -4],

A solution set is:
[
  [-1, 0, 1],
  [-1, -1, 2]
]

Solution:

To simplify the problem, sort the nums first.

If sorted[0] > 0 or sorted[last] < 0, return an empty set.

From i = 0 to len(sorted) - 2, pick sorted[i] as the first number of a possible triplet result.

Let l = i + 1, r = len(sorted) - 1, we want to narrow them down to enumerate all possible combinations.

• l++ if sorted[i] + sorted[l] + sorted[r] > 0.
• r-- if sorted[i] + sorted[l] + sorted[r] < 0.

Skip any duplicate number as we iterate to avoid duplicate triplets.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let threeSum = function (nums) {
  const len = nums.length
  const sorted = nums.sort((a, b) => a - b)
  const result = []

  if (sorted[0] > 0 || sorted[len-1] < 0) {
    return result
  }

  for (let i = 0; i < len - 2; i++) {
    if (sorted[i] > 0) {
      break
    }

    if (i > 0 && sorted[i] === sorted[i-1]) {
      continue
    }

    const twoSum = 0 - sorted[i]

    for (let l = i + 1, r = len - 1; l < r;) {
      const diff = twoSum - sorted[l] - sorted[r]
      if (diff > 0) {
        l++
      } else if (diff < 0) {
        r--
      } else {
        result.push([sorted[i], sorted[l], sorted[r]])
        while (++l < r && sorted[l] === sorted[l - 1]);
        while (--r > l && sorted[r] === sorted[r + 1]);
      }
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “3Sum”: https://leetcode.com/problems/3sum “3Sum Smaller”: https://leetcode.com/problems/3sum-smaller

16. 3Sum Closest

Problem:

Given an array nums of n integers and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution.

Example:

Given array nums = [-1, 2, 1, -4], and target = 1.

The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).

Solution:

Simplified version of 15. 3Sum.

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
let threeSumClosest = function(nums, target) {
  const len = nums.length
  const sorted = nums.sort((a, b) => a - b)

  let minDiff = Infinity

  for (let i = 0; i < len - 2; i++) {
    if (i > 0 && sorted[i] === sorted[i-1]) {
      continue
    }

    const twoSum = target - sorted[i]

    for (let l = i + 1, r = len - 1; l < r;) {
      const diff = twoSum - sorted[l] - sorted[r]
      if (diff === 0) {
        return target
      } else {
        if (diff > 0) {
          l++
        } else {
          r--
        }

        if (Math.abs(diff) < Math.abs(minDiff)) {
          minDiff = diff
        }
      }
    }
  }

  return target - minDiff
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “String”: https://leetcode.com/tag/string “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Generate Parentheses”: https://leetcode.com/problems/generate-parentheses “Combination Sum”: https://leetcode.com/problems/combination-sum “Binary Watch”: https://leetcode.com/problems/binary-watch

17. Letter Combinations of a Phone Number

Problem:

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.

A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Example:

Input: "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

Note:

Although the above answer is in lexicographical order, your answer could be in any order you want.

Solution:

ONE

JavaScript specific optimization.

Array.prototype.push accepts arbitrary arguments which enables tighter loops.

Also, appending string is faster than prepending.

/**
 * @param {string} digits
 * @return {string[]}
 */
let letterCombinations = function(digits) {
  if (digits.length <= 0) { return [] }

  const letters = [
    ,
    ,
    ['a', 'b', 'c'],
    ['d', 'e', 'f'],
    ['g', 'h', 'i'],
    ['j', 'k', 'l'],
    ['m', 'n', 'o'],
    ['p', 'q', 'r', 's'],
    ['t', 'u', 'v'],
    ['w', 'x', 'y', 'z'],
  ]

  let result = ['']

  for (let i = 0; i < digits.length; i++) {
    const arr = letters[digits[i]]
    let newResult = []
    arr.forEach(c => newResult.push(...result.map(r => r + c)))
    result = newResult
  }

  return result
};

TWO

General recursive DFS solution.

/**
 * @param {string} digits
 * @return {string[]}
 */
let letterCombinations = function(digits) {
  const letters = [,, 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
  const result = []
  if (digits.length > 0) {
    dfs(digits, 0, '', letters, result)
  }
  return result
};

function dfs (digits, idigit, path, letters, result) {
  if (idigit >= digits.length) {
    result.push(path)
    return
  }
  const str = letters[digits[idigit]]
  for (let i = 0; i < str.length; i++) {
    dfs(digits, idigit + 1, path + str[i], letters, result)
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Hash Table”: https://leetcode.com/tag/hash-table “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Two Sum”: https://leetcode.com/problems/two-sum “3Sum”: https://leetcode.com/problems/3sum “4Sum II”: https://leetcode.com/problems/4sum-ii

18. 4Sum

Problem:

Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.

Note:

The solution set must not contain duplicate quadruplets.

Example:

Given array nums = [1, 0, -1, 0, -2, 2], and target = 0.

A solution set is:
[
  [-1,  0, 0, 1],
  [-2, -1, 1, 2],
  [-2,  0, 0, 2]
]

Solution:

Like 15. 3Sum and 16. 3Sum Closest. Wrap one more loop.

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[][]}
 */
let fourSum = function(nums, target) {
  const len = nums.length
  const sorted = nums.sort((a, b) => a - b)
  const result = []

  for (let k = 0; k < len - 3; k++) {
    if (k > 0 && sorted[k] === sorted[k-1]) {
      continue
    }

    const threeSum = target - sorted[k]

    for (let i = k+1; i < len - 2; i++) {
      if (i > k+1 && sorted[i] === sorted[i-1]) {
        continue
      }

      const twoSum = threeSum - sorted[i]

      for (let l = i + 1, r = len - 1; l < r;) {
        const diff = twoSum - sorted[l] - sorted[r]
        if (diff > 0) {
          l++
        } else if (diff < 0) {
          r--
        } else {
          result.push([sorted[k], sorted[i], sorted[l], sorted[r]])
          while (++l < r && sorted[l] === sorted[l - 1]);
          while (--r > l && sorted[r] === sorted[r + 1]);
        }
      }
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Linked List”: https://leetcode.com/tag/linked-list “Two Pointers”: https://leetcode.com/tag/two-pointers

19. Remove Nth Node From End of List

Problem:

Given a linked list, remove the n-th node from the end of list and return its head.

Example:

Given linked list: 1->2->3->4->5, and n = 2.

After removing the second node from the end, the linked list becomes 1->2->3->5.

Note:

Given n will always be valid.

Follow up:

Could you do this in one pass?

Solution:

Set a pointer p1 for iterating, and p2 which is n nodes behind, pointing at the (n+1)-th node from the end of list.

Boundaries that should be awared of:

• p2 could be one node before head, which means the head should be removed.
• p2 could be larger than the length of the list (Though the description says n will always be valid, we take care of it anyway).
• It should be p1.next touches the end rather than p1 because we want p1 pointing at the last node.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} n
 * @return {ListNode}
 */
let removeNthFromEnd = function(head, n) {
  let p1 = head
  while (p1 && n--) {
    p1 = p1.next
  }

  if (!p1) { return n ? head : head.next }

  let p2 = head
  while (p1.next) {
    p1 = p1.next
    p2 = p2.next
  }

  p2.next = p2.next.next

  return head
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “String”: https://leetcode.com/tag/string “Stack”: https://leetcode.com/tag/stack Similar Questions: “Generate Parentheses”: https://leetcode.com/problems/generate-parentheses “Longest Valid Parentheses”: https://leetcode.com/problems/longest-valid-parentheses “Remove Invalid Parentheses”: https://leetcode.com/problems/remove-invalid-parentheses

20. Valid Parentheses

Problem:

Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.

Note that an empty string is also considered valid.

Example 1:

Input: "()"
Output: true

Example 2:

Input: "()[]{}"
Output: true

Example 3:

Input: "(]"
Output: false

Example 4:

Input: "([)]"
Output: false

Example 5:

Input: "{[]}"
Output: true

Solution:

Stack 101.

Whenever we meet a close bracket, we want to compare it to the last open bracket.

That is why we use stack to store open brackets: first in, last out.

And since there is only bracket characters, the last open bracket happens to be the last character.

/**
 * @param {string} s
 * @return {boolean}
 */
let isValid = function(s) {
  const stack = []
  const pairs = {
    '}': '{',
    ']': '[',
    ')': '(',
  }
  for (const c of s) {
    const open = pairs[c]
    if (open) {
      if (stack.pop() !== open) {
        return false
      }
    } else {
      stack.push(c)
    }
  }
  return stack.length <= 0
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Linked List”: https://leetcode.com/tag/linked-list Similar Questions: “Merge k Sorted Lists”: https://leetcode.com/problems/merge-k-sorted-lists “Merge Sorted Array”: https://leetcode.com/problems/merge-sorted-array “Sort List”: https://leetcode.com/problems/sort-list “Shortest Word Distance II”: https://leetcode.com/problems/shortest-word-distance-ii

21. Merge Two Sorted Lists

Problem:

Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.

Example:

Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4

Solution:

Keep tracking the head of two lists and keep moving the pointer of smaller one to the next node.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
let mergeTwoLists = function(l1, l2) {
  let prehead = { next: null }
  let p = prehead
  let p1 = l1
  let p2 = l2
  while (p1 && p2) {
    let pSel
    if  (p1.val < p2.val) {
      pSel = p1
      p1 = p1.next
    } else {
      pSel = p2
      p2 = p2.next
    }
    p.next = pSel
    p = pSel
  }

  p.next = p1 || p2

  return prehead.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “String”: https://leetcode.com/tag/string “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Letter Combinations of a Phone Number”: https://leetcode.com/problems/letter-combinations-of-a-phone-number “Valid Parentheses”: https://leetcode.com/problems/valid-parentheses

22. Generate Parentheses

Problem:

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

For example, given n = 3, a solution set is:

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

Solution:

ONE

Recursive DFS backtracking.

/**
 * @param {number} n
 * @return {string[]}
 */
let generateParenthesis = function(n) {
  const result = []
  if (n > 0) {
    dfs(n, 0, 0, '', result)
  }
  return result
};

function dfs (n, nopen, nclose, path, result) {
  if (path.length === n * 2) {
    result.push(path)
    return
  }

  if (nopen < n) {
    dfs(n, nopen + 1, nclose, path + '(', result)
  }

  if (nclose < nopen) {
    dfs(n, nopen, nclose + 1, path + ')', result)
  }
};

TWO

BFS.

/**
 * @param {number} n
 * @return {string[]}
 */
let generateParenthesis = function(n) {
  if (n <= 0) { return [] }

  const queue = [{
    path: '(',
    open: 1,
    close: 0,
  }]

  while (true) {
    const { path, open, close } = queue.shift()
    if (open + close === n * 2) {
      queue.unshift({ path, open, close })
      break
    }

    if (open < n) {
      queue.push({
        path: path + '(',
        open: open + 1,
        close,
      })
    }

    if (close < open) {
      queue.push({
        path: path + ')',
        open,
        close: close + 1,
      })
    }
  }

  return queue.map(x => x.path)
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Linked List”: https://leetcode.com/tag/linked-list “Divide and Conquer”: https://leetcode.com/tag/divide-and-conquer “Heap”: https://leetcode.com/tag/heap Similar Questions: “Merge Two Sorted Lists”: https://leetcode.com/problems/merge-two-sorted-lists “Ugly Number II”: https://leetcode.com/problems/ugly-number-ii

23. Merge k Sorted Lists

Problem:

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

Example:

Input:
[
  1->4->5,
  1->3->4,
  2->6
]
Output: 1->1->2->3->4->4->5->6

Solution:

ONE

Extend the idea of 21. Merge Two Sorted Lists and compare N items at a time.

This is slow as it reaches O(N^2).

TWO

Priority Queue. O(N * log(K)).

Since JavaScript does not provide a standard built-in Priority Queue data structure, it is challenging to implement an efficient one barehanded.

THREE

Divide and conquer. Also O(N * log(K)).

Divide N lists into ceil(N/2) pairs and merge your way up.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
let mergeKLists = function(lists) {
  while (lists.length > 1) {
    lists.unshift(mergeTwoLists(lists.pop(), lists.pop()))
  }
  return lists[0] || []
};

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
function mergeTwoLists (l1, l2) {
  let prehead = { next: null }
  let p = prehead
  let p1 = l1
  let p2 = l2
  while (p1 && p2) {
    let pSel
    if  (p1.val < p2.val) {
      pSel = p1
      p1 = p1.next
    } else {
      pSel = p2
      p2 = p2.next
    }
    p.next = pSel
    p = pSel
  }

  p.next = p1 || p2

  return prehead.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Linked List”: https://leetcode.com/tag/linked-list Similar Questions: “Reverse Nodes in k-Group”: https://leetcode.com/problems/reverse-nodes-in-k-group

24. Swap Nodes in Pairs

Problem:

Given a linked list, swap every two adjacent nodes and return its head.

Example:

Given 1->2->3->4, you should return the list as 2->1->4->3.

Note:

• Your algorithm should use only constant extra space.
• You may not modify the values in the list’s nodes, only nodes itself may be changed.

Solution:

1. Draw the nodes down on paper to reason about the relationships.
2. Pointing to every active node is an easy way to keep on track.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
let swapPairs = function(head) {
  const prehead = { next: head }

  for (let p = prehead; p.next !== null && p.next.next !== null;) {
    const p1 = p.next
    const p2 = p1.next
    p1.next = p2.next
    p2.next = p1
    p.next = p2
    p = p1
  }

  return prehead.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Linked List”: https://leetcode.com/tag/linked-list Similar Questions: “Swap Nodes in Pairs”: https://leetcode.com/problems/swap-nodes-in-pairs

25. Reverse Nodes in k-Group

Problem:

Given a linked list, reverse the nodes of a linked list k at a time and return its modified list.

k is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of k then left-out nodes in the end should remain as it is.

Example:

Given this linked list: 1->2->3->4->5

For k = 2, you should return: 2->1->4->3->5

For k = 3, you should return: 3->2->1->4->5

Note:

• Only constant extra memory is allowed.
• You may not alter the values in the list’s nodes, only nodes itself may be changed.

Solution:

1. Find the end node of a portion that needs to be reversed.
2. Get the next node of the end node.
3. Reverse the portion using the next node as edge(null) pointer.
4. Connect it back to the main linked list.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
let reverseKGroup = function(head, k) {
  const prehead = { next: head }
  let p = prehead
  while (true) {
    let n = k
    let pEndNext = p.next
    while (pEndNext && n) {
      pEndNext = pEndNext.next
      n--
    }

    if (n !== 0) {
      break
    }

    const nextp = p.next // The first node will be the last after reverse
    p.next = reverseLinkList(p.next, pEndNext)
    p = nextp
  }

  return prehead.next
};

function reverseLinkList (head, nullNode = null) {
  let prev = nullNode
  let curr = head
  while (curr !== nullNode) {
    const next = curr.next
    curr.next = prev
    prev = curr
    curr = next
  }
  return prev
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Remove Element”: https://leetcode.com/problems/remove-element “Remove Duplicates from Sorted Array II”: https://leetcode.com/problems/remove-duplicates-from-sorted-array-ii

26. Remove Duplicates from Sorted Array

Problem:

Given a sorted array nums, remove the duplicates in-place such that each element appear only once and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Example 1:

Given nums = [1,1,2],

Your function should return length = 2, with the first two elements of nums being 1 and 2 respectively.

It doesn't matter what you leave beyond the returned length.

Example 2:

Given nums = [0,0,1,1,1,2,2,3,3,4],

Your function should return length = 5, with the first five elements of nums being modified to 0, 1, 2, 3, and 4 respectively.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy)
int len = removeDuplicates(nums);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

Solution:

The result array can only be shorter. That is why we can build the array in-place with the new length.

/**
 * @param {number[]} nums
 * @return {number}
 */
let removeDuplicates = function(nums) {
  let len = 0
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] !== nums[i-1]) {
      nums[len++] = nums[i]
    }
  }
  return len
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Remove Duplicates from Sorted Array”: https://leetcode.com/problems/remove-duplicates-from-sorted-array “Remove Linked List Elements”: https://leetcode.com/problems/remove-linked-list-elements “Move Zeroes”: https://leetcode.com/problems/move-zeroes

27. Remove Element

Problem:

Given an array nums and a value val, remove all instances of that value in-place and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

The order of elements can be changed. It doesn’t matter what you leave beyond the new length.

Example 1:

Given nums = [3,2,2,3], val = 3,

Your function should return length = 2, with the first two elements of nums being 2.

It doesn't matter what you leave beyond the returned length.

Example 2:

Given nums = [0,1,2,2,3,0,4,2], val = 2,

Your function should return length = 5, with the first five elements of nums containing 0, 1, 3, 0, and 4.

Note that the order of those five elements can be arbitrary.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy)
int len = removeElement(nums, val);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

Solution:

The order does not matter. So just take the last number to fill the vacancy.

/**
 * @param {number[]} nums
 * @param {number} val
 * @return {number}
 */
let removeElement = function(nums, val) {
  let len = nums.length
  for (let i = 0; i < len; i++) {
    if (nums[i] === val) {
      nums[i--] = nums[--len]
    }
  }
  return len
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Math”: https://leetcode.com/tag/math “Binary Search”: https://leetcode.com/tag/binary-search

29. Divide Two Integers

Problem:

Given two integers dividend and divisor, divide two integers without using multiplication, division and mod operator.

Return the quotient after dividing dividend by divisor.

The integer division should truncate toward zero.

Example 1:

Input: dividend = 10, divisor = 3
Output: 3

Example 2:

Input: dividend = 7, divisor = -3
Output: -2

Note:

• Both dividend and divisor will be 32-bit signed integers.
• The divisor will never be 0.
• Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−231,  231 − 1]. For the purpose of this problem, assume that your function returns 231 − 1 when the division result overflows.

Solution:

Every decimal number can be represented as a0*2^0 + a1*2^1 + a2*2^2 + ... + an*2^n.

Replace multiplication and division with binary shifting.

/**
 * @param {number} dividend
 * @param {number} divisor
 * @return {number}
 */
let divide = function(dividend, divisor) {
  if (divisor === 0 ||
      divisor === -1 && dividend < -2147483647 ||
      dividend > 2147483647 ||
      dividend < -2147483648
  ) {
    return 2147483647
  }

  const isNegative = dividend < 0 && divisor >= 0 || dividend >= 0 && divisor < 0
  const pDividend = Math.abs(dividend)
  const pDivisor = Math.abs(divisor)

  if (dividend === 0 || pDividend < pDivisor) { return 0 }

  let doubling = pDivisor
  let count = 1
  while (doubling < pDividend && !(doubling & (1 << 30))) {
    doubling <<= 1
    count <<= 1
  }
  if (doubling > pDividend) {
    doubling >>>= 1
    count >>>= 1
  }

  const result = count + divide(pDividend - doubling, pDivisor)
  return isNegative ? -result : result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Permutations”: https://leetcode.com/problems/permutations “Permutations II”: https://leetcode.com/problems/permutations-ii “Permutation Sequence”: https://leetcode.com/problems/permutation-sequence “Palindrome Permutation II”: https://leetcode.com/problems/palindrome-permutation-ii

31. Next Permutation

Problem:

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.

If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).

The replacement must be in-place and use only constant extra memory.

Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.

1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

Solution:

Observe a few longer examples and the pattern is self-evident.

Divide the list into two parts. The first half must be incremental and the second half must be decremental.

Reverse the second half and find the smallest number in it that is greater the last number of the first half.

Swap the two.

/**
 * @param {number[]} nums
 * @return {void} Do not return anything, modify nums in-place instead.
 */
let nextPermutation = function(nums) {
  const len = nums.length
  if (len <= 1) { return }

  for (let i = len - 1; i > 0; i--) {
    if (nums[i] > nums[i-1]) {
      let t
      for (let s = i, e = len-1; s < e; s++, e--) {
        t = nums[s]
        nums[s] = nums[e]
        nums[e]  = t
      }

      let j = len - 1
      while (nums[j] <= nums[i-1]) {
        j--
      }

      t = nums[j]
      nums[j] = nums[i-1]
      nums[i-1] = t

      break
    }
  }

  if (i === 0) {
    nums.reverse()
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “Search in Rotated Sorted Array II”: https://leetcode.com/problems/search-in-rotated-sorted-array-ii “Find Minimum in Rotated Sorted Array”: https://leetcode.com/problems/find-minimum-in-rotated-sorted-array

33. Search in Rotated Sorted Array

Problem:

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm’s runtime complexity must be in the order of O(log n).

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Solution:

Obviously the problem requires binary search.

The core idea of binary search is to pick the middle item and then decide to keep which half.

The precondition of it is the array must be sorted.

But take a closer look and we realize that only one of the two halves needs to be sorted. This is sufficient for us to know if the target is in that half. If not, then it must be in the other.

Whenever we choose a pivot, it must be in one of the two sorted parts of the rotated array.

• If the pivot is in the left part. We know that the begin of the left part to the pivot are sorted.
• Otherwise the pivot is in the right part. We know that the end of the right part to the pivot are sorted.

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
let search = function(nums, target) {
  let s = 0
  let e = nums.length - 1

  while (s <= e) {
    const p = (e + s) / 2 | 0
    const pivot = nums[p]

    if (pivot === target) {
      return p
    }

    if (pivot < nums[e]) {
      // right half is sorted
      if (target > pivot  && target <= nums[e]) {
        // target is inside the right half
        s = p + 1
      } else {
        e = p - 1
      }
    } else {
      // left half is sorted
      if (target < pivot && target >= nums[s]) {
        // target is inside the left half
        e = p - 1
      } else {
        s = p + 1
      }
    }
  }

  return -1
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “First Bad Version”: https://leetcode.com/problems/first-bad-version

34. Find First and Last Position of Element in Sorted Array

Problem:

Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.

Your algorithm’s runtime complexity must be in the order of O(log n).

If the target is not found in the array, return [-1, -1].

Example 1:

Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]

Example 2:

Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]

Solution:

Implement two variations of binary search to get the first and last matching positions.

They are basically the same as simple binary search except when we got the match, we mark the index and keep moving forward.

If we want to get the first, we dump the right half. Vice versa.

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
let searchRange = function(nums, target) {
  let s = 0
  let e = nums.length - 1

  const first = searchFirst(nums, target, 0, nums.length - 1)

  if (first === -1) {
    return [-1, -1]
  }

  return [first, searchLast(nums, target, first, nums.length - 1)]
};

function searchFirst (nums, target, s, e) {
  let result = -1

  while (s <= e) {
    const p = (s + e) / 2 | 0
    const diff = nums[p] - target
    if (diff === 0) {
      result = p
      e = p - 1
    } else if (diff > 0) {
      e = p - 1
    } else {
      s = s + 1
    }
  }

  return result
};

function searchLast (nums, target, s, e) {
  let result = -1

  while (s <= e) {
    const p = (s + e) / 2 | 0
    const diff = nums[p] - target
    if (diff === 0) {
      result = p
      s = p + 1
    } else if (diff > 0) {
      e = p - 1
    } else {
      s = s + 1
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “First Bad Version”: https://leetcode.com/problems/first-bad-version

35. Search Insert Position

Problem:

Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You may assume no duplicates in the array.

Example 1:

Input: [1,3,5,6], 5
Output: 2

Example 2:

Input: [1,3,5,6], 2
Output: 1

Example 3:

Input: [1,3,5,6], 7
Output: 4

Example 4:

Input: [1,3,5,6], 0
Output: 0

Solution:

Same as simple binary search except it returns the start index when does not find a match.

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
let searchInsert = function(nums, target) {
  let s = 0
  let e = nums.length - 1

  while (s <= e) {
    const p = (s + e) / 2 | 0
    const diff = nums[p] - target
    if (diff === 0) {
      return p
    } else if (diff < 0) {
      s = p + 1
    } else {
      e = p - 1
    }
  }

  return s
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Hash Table”: https://leetcode.com/tag/hash-table Similar Questions: “Sudoku Solver”: https://leetcode.com/problems/sudoku-solver

36. Valid Sudoku

Problem:

Determine if a 9x9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:

1. Each row must contain the digits 1-9 without repetition.
2. Each column must contain the digits 1-9 without repetition.
3. Each of the 9 3x3 sub-boxes of the grid must contain the digits 1-9 without repetition.

A partially filled sudoku which is valid.

The Sudoku board could be partially filled, where empty cells are filled with the character '.'.

Example 1:

Input:
[
  ["5","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
Output: true

Example 2:

Input:
[
  ["8","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being
    modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.

Note:

• A Sudoku board (partially filled) could be valid but is not necessarily solvable.
• Only the filled cells need to be validated according to the mentioned rules.
• The given board contain only digits 1-9 and the character '.'.
• The given board size is always 9x9.

Solution:

Scan the board once.

/**
 * @param {character[][]} board
 * @return {boolean}
 */
let isValidSudoku = function(board) {
  if (!board || board.length !== 9) { return false }

  const newArray = () => []
  const col = board.map(newArray)
  const row = board.map(newArray)
  const sub = board.map(newArray)

  for (let r = 0; r < 9; r++) {
    if (board[r].length !== 9) { return false }

    for (let c = 0; c < 9; c++) {
      const num = board[r][c]
      const subOffset = 3 * (r / 3 | 0) + (c / 3 | 0)
      if (num !== '.') {
        if (!(num >= 1 && num <= 9) ||
            row[r][num] ||
            col[c][num] ||
            sub[subOffset][num]
        ) {
          return false
        }
        row[r][num] = true
        col[c][num] = true
        sub[subOffset][num] = true
      }
    }
  }

  return true
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Hash Table”: https://leetcode.com/tag/hash-table “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Valid Sudoku”: https://leetcode.com/problems/valid-sudoku

37. Sudoku Solver

Problem:

Write a program to solve a Sudoku puzzle by filling the empty cells.

A sudoku solution must satisfy all of the following rules:

1. Each of the digits 1-9 must occur exactly once in each row.
2. Each of the digits 1-9 must occur exactly once in each column.
3. Each of the the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

Empty cells are indicated by the character '.'.

A sudoku puzzle…

…and its solution numbers marked in red.

Note:

• The given board contain only digits 1-9 and the character '.'.
• You may assume that the given Sudoku puzzle will have a single unique solution.
• The given board size is always 9x9.

Solution:

DFS + backtracking.

Just like 36. Valid Sudoku but instead of validating the board with three tables, we use these three tables to get all the valid numbers at a position. This is super fast as it skips a lot of redundant comparisons.

Every time we reach a position, we pick a possible solution and move on to the next position, which is an identical problem.

If the next position fails, we come back and try the next possible solution of the current position.

If all possible solutions fail, we just dump the current position and go back to the last position.

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
let solveSudoku = function(board) {
  const newArray = () => []
  const col = board.map(newArray)
  const row = board.map(newArray)
  const sub = board.map(newArray)

  for (let r = 0; r < 9; r++) {
    for (let c = 0; c < 9; c++) {
      const num = +board[r][c]
      if (num) {
        const subOffset = 3 * (r / 3 | 0) + (c / 3 | 0)
        row[r][num] = true
        col[c][num] = true
        sub[subOffset][num] = true
      }
    }
  }

  dfs(board, col, row, sub, 0)
};

function dfs (board, col, row, sub, pos) {
  if  (pos >= 81) { return true }

  const r = pos / 9 | 0
  const c = pos % 9

  if (board[r][c] !== '.') {
    return dfs(board, col, row, sub, pos + 1)
  }

  const subOffset = 3 * (r / 3 | 0) + (c / 3 | 0)

  for (let num = 1; num <= 9; num++) {
    if (!(row[r][num] || col[c][num] || sub[subOffset][num])) {
      row[r][num] = true
      col[c][num] = true
      sub[subOffset][num] = true

      if (dfs(board, col, row, sub, pos + 1)) {
        board[r][c] = num + ''
        return true
      } else {
        row[r][num] = false
        col[c][num] = false
        sub[subOffset][num] = false
      }
    }
  }

  return false
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “String”: https://leetcode.com/tag/string Similar Questions: “Encode and Decode Strings”: https://leetcode.com/problems/encode-and-decode-strings “String Compression”: https://leetcode.com/problems/string-compression

38. Count and Say

Problem:

The count-and-say sequence is the sequence of integers with the first five terms as following:

1.     1
2.     11
3.     21
4.     1211
5.     111221

1 is read off as "one 1" or 11.
11 is read off as "two 1s" or 21.
21 is read off as "one 2, then one 1" or 1211.

Given an integer n, generate the nth term of the count-and-say sequence.

Note: Each term of the sequence of integers will be represented as a string.

Example 1:

Input: 1
Output: "1"

Example 2:

Input: 4
Output: "1211"

Solution:

Just loop and grow the sequence.

ONE

JavaScript specific.

/**
 * @param {number} n
 * @return {string}
 */
let countAndSay = function(n) {
  let num = '1'

  while (--n > 0) {
    num = num.match(/(\d)\1*/g).map(x => x.length + x[0]).join('')
  }

  return num
};

TWO

General solution.

/**
 * @param {number} n
 * @return {string}
 */
let countAndSay = function(n) {
  let num = '1'

  while (--n > 0) {
    let newNum = ''
    for (let i = 0, accu = 1; i < num.length; i++, accu++) {
      if (num[i] !== num[i+1]) {
        newNum += accu + num[i]
        accu = 0
      }
    }
    num = newNum
  }

  return num
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Letter Combinations of a Phone Number”: https://leetcode.com/problems/letter-combinations-of-a-phone-number “Combination Sum II”: https://leetcode.com/problems/combination-sum-ii “Combinations”: https://leetcode.com/problems/combinations “Combination Sum III”: https://leetcode.com/problems/combination-sum-iii “Factor Combinations”: https://leetcode.com/problems/factor-combinations “Combination Sum IV”: https://leetcode.com/problems/combination-sum-iv

39. Combination Sum

Problem:

Given a set of candidate numbers (candidates) (without duplicates) and a target number (target), find all unique combinations in candidates where the candidate numbers sums to target.

The same repeated number may be chosen from candidates unlimited number of times.

Note:

• All numbers (including target) will be positive integers.
• The solution set must not contain duplicate combinations.

Example 1:

Input: candidates = [2,3,6,7], target = 7,
A solution set is:
[
  [7],
  [2,2,3]
]

Example 2:

Input: candidates = [2,3,5], target = 8,
A solution set is:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

Solution:

DFS + Backtracking.

To prevent duplications, only loop the right side of the candidates.

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
let combinationSum = function(candidates, target) {
  return dfs(candidates, target, [], [], 0)
};

function dfs (candidates, target, result, path, start) {
  for (let i = start; i < candidates.length; i++) {
    const cand = candidates[i]

    if (cand > target) {
      continue
    }

    path.push(cand)
    if (cand === target) {
      result.push(path.slice())
    } else {
      dfs(candidates, target - cand, result, path, i)
    }
    path.pop(cand)
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Combination Sum”: https://leetcode.com/problems/combination-sum

40. Combination Sum II

Problem:

Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sums to target.

Each number in candidates may only be used once in the combination.

Note:

• All numbers (including target) will be positive integers.
• The solution set must not contain duplicate combinations.

Example 1:

Input: candidates = [10,1,2,7,6,1,5], target = 8,
A solution set is:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

Example 2:

Input: candidates = [2,5,2,1,2], target = 5,
A solution set is:
[
  [1,2,2],
  [5]
]

Solution:

Mostly the same as 39. Combination Sum.

Now the candidates might have duplicate numbers, so we need to sort it.

We can also safely return when number is larger than the target.

To prvent duplicate results, stop searching if the current number is same as the last.

Notice the number at start is immune by the rule because we assume that the current group of candidates begins at start.

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
let combinationSum2 = function(candidates, target) {
  return dfs(candidates.sort((a, b) => a - b), target, [], [], 0)
};

function dfs (candidates, target, result, path, start) {
  for (let i = start; i < candidates.length; i++) {
    const cand = candidates[i]

    if (cand > target) {
      return result
    }

    if (i > start && cand === candidates[i-1]) {
      continue
    }

    path.push(cand)
    if (cand === target) {
      result.push(path.slice())
    } else {
      dfs(candidates, target - cand, result, path, i + 1)
    }
    path.pop()
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Missing Number”: https://leetcode.com/problems/missing-number “Find the Duplicate Number”: https://leetcode.com/problems/find-the-duplicate-number “Find All Numbers Disappeared in an Array”: https://leetcode.com/problems/find-all-numbers-disappeared-in-an-array “Couples Holding Hands”: https://leetcode.com/problems/couples-holding-hands

41. First Missing Positive

Problem:

Given an unsorted integer array, find the smallest missing positive integer.

Example 1:

Input: [1,2,0]
Output: 3

Example 2:

Input: [3,4,-1,1]
Output: 2

Example 3:

Input: [7,8,9,11,12]
Output: 1

Note:

Your algorithm should run in O(n) time and uses constant extra space.

Solution:

The last requirement is why this problem is marked “hard”. Though the solution feels like cheating: it modifies the array to mark numbers.

So the algorithm still requires O(n) space but O(1) extra space.

The core idea of the solution is, if the length of the array is n, then the smallest missing positive integer must be within [1, n+1].

Consider an edge-case scenario where the array is [1,2,...,n]. The smallest missing positive integer is n+1.

Now if one of these integers is missing in the array, that integer is the smallest missing positive integer.

If more than one are missing, pick the smallest.

So here we reuse the array and keep trying to put integer k into the slot indexed k-1 (via swapping).

/**
 * @param {number[]} nums
 * @return {number}
 */
let firstMissingPositive = function(nums) {
  const n = nums.length

  for (let i = 1; i < n; i++) {
    while (nums[i] <= n && nums[i] !== nums[nums[i] - 1]) {
      const t = nums[i]
      nums[i] = nums[t - 1]
      nums[t - 1] = t
    }
  }

  for (let i = 0; i < n; i++) {
    if (nums[i] !== i + 1) {
      return i + 1
    }
  }

  return n + 1
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers “Stack”: https://leetcode.com/tag/stack Similar Questions: “Container With Most Water”: https://leetcode.com/problems/CONTENT-with-most-water “Product of Array Except Self”: https://leetcode.com/problems/product-of-array-except-self “Trapping Rain Water II”: https://leetcode.com/problems/trapping-rain-water-ii “Pour Water”: https://leetcode.com/problems/pour-water

42. Trapping Rain Water

Problem:

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

Solution:

Well explained by Leetcode official: https://leetcode.com/articles/trapping-rain-water/ .

/**
 * @param {number[]} height
 * @return {number}
 */
let trap = function(height) {
  let i = 0
  let j = height.length - 1
  let lMax = 0
  let rMax = 0
  let result = 0

  while (i < j) {
    const left = height[i]
    const right = height[j]
    if (left < right) {
      if (left < lMax) {
        result += lMax - left
      } else {
        lMax = left
      }
      i++
    } else {
      if (right < rMax) {
        result += rMax - right
      } else {
        rMax = right
      }
      j--
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Math”: https://leetcode.com/tag/math “String”: https://leetcode.com/tag/string Similar Questions: “Add Two Numbers”: https://leetcode.com/problems/add-two-numbers “Plus One”: https://leetcode.com/problems/plus-one “Add Binary”: https://leetcode.com/problems/add-binary “Add Strings”: https://leetcode.com/problems/add-strings

43. Multiply Strings

Problem:

Given two non-negative integers num1 and num2 represented as strings, return the product of num1 and num2, also represented as a string.

Example 1:

Input: num1 = "2", num2 = "3"
Output: "6"

Example 2:

Input: num1 = "123", num2 = "456"
Output: "56088"

Note:

1. The length of both num1 and num2 is < 110.
2. Both num1 and num2 contain only digits 0-9.
3. Both num1 and num2 do not contain any leading zero, except the number 0 itself.
4. You must not use any built-in BigInteger library or convert the inputs to integer directly.

Solution:

Same as we do multiplication on a paper.

/**
 * @param {string} num1
 * @param {string} num2
 * @return {string}
 */
let multiply = function(num1, num2) {
  const result = []

  for (i = num1.length - 1; i >= 0; i--) {
    for (j = num2.length - 1; j >= 0; j--) {
      const sum = num1[i] * num2[j] + (result[i+j+1] || 0)
      result[i+j] = (sum / 10 | 0) + (result[i+j] || 0)
      result[i+j+1] = sum % 10
    }
  }

  return result.join('').replace(/^0+(?=[0-9])/, '')
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Greedy”: https://leetcode.com/tag/greedy Similar Questions: “Jump Game”: https://leetcode.com/problems/jump-game

45. Jump Game II

Problem:

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Your goal is to reach the last index in the minimum number of jumps.

Example:

Input: [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2.
    Jump 1 step from index 0 to 1, then 3 steps to the last index.

Note:

You can assume that you can always reach the last index.

Solution:

Greedy. Always pick the one that would allow to jump to the rightest.

/**
 * @param {number[]} nums
 * @return {number}
 */
let jump = function(nums) {
  const len = nums.length
  let jump = 0
  for (let l = 0, r = 1; r < len; jump++) {
    let rNext = r
    for (let i = l; i < r; i++) {
      const rNextAtmp = i + nums[i] + 1
      if (rNextAtmp > rNext) {
        rNext = rNextAtmp
      }
    }
    l = r
    r = rNext
  }
  return jump
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Next Permutation”: https://leetcode.com/problems/next-permutation “Permutations II”: https://leetcode.com/problems/permutations-ii “Permutation Sequence”: https://leetcode.com/problems/permutation-sequence “Combinations”: https://leetcode.com/problems/combinations

46. Permutations

Problem:

Given a collection of distinct integers, return all possible permutations.

Example:

Input: [1,2,3]
Output:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

Solution:

One position at a time, pick a number from the unused set and put it in that position (by swapping). Then move on to the next.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let permute = function(nums) {
  const result = []
  _permute(nums, 0, result)
  return result
};

function _permute (nums, start, result) {
  if (start === nums.length) {
    return result.push(nums.slice())
  }

  const begin = nums[start]
  for (let i = start; i < nums.length; i++) {
    const next = nums[i]

    nums[start] = next
    nums[i] = begin

    _permute(nums, start + 1, result)

    nums[start] = begin
    nums[i] = next
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Next Permutation”: https://leetcode.com/problems/next-permutation “Permutations”: https://leetcode.com/problems/permutations “Palindrome Permutation II”: https://leetcode.com/problems/palindrome-permutation-ii

47. Permutations II

Problem:

Given a collection of numbers that might contain duplicates, return all possible unique permutations.

Example:

Input: [1,1,2]
Output:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

Solution:

Same as 46. Permutations. To avoid duplication, when picking a number for a position, only pick the unused. Either sort the nums or use a set to mark.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let permuteUnique = function(nums) {
  const result = []
  _permuteUnique(nums, 0, result)
  return result
};

function _permuteUnique (nums, start, result) {
  if (start === nums.length) {
    result.push(nums.slice())
  }

  const used = new Set()
  const begin = nums[start]
  for (let i = start; i < nums.length; i++) {
    const next = nums[i]

    if (used.has(next)) {
      continue
    }

    used.add(next)

    nums[start] = next
    nums[i] = begin

    _permuteUnique(nums, start + 1, result)

    nums[start] = begin
    nums[i] = next
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array

48. Rotate Image

Problem:

You are given an n x n 2D matrix representing an image.

Rotate the image by 90 degrees (clockwise).

Note:

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

Given input matrix =
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

rotate the input matrix in-place such that it becomes:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

Example 2:

Given input matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
],

rotate the input matrix in-place such that it becomes:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

Solution:

Outside-in. Rotate one square at a time.

/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
let rotate = function(matrix) {
  if (!matrix || matrix.length <= 0) {
    return
  }
  const width = matrix.length
  const halfWidthFloor = Math.floor(width / 2)
  const halfWidthCeil = Math.ceil(width / 2)
  for (let i = 0; i < halfWidthFloor; i++) {
    const iend = width - 1 - i
    for (let j = 0; j < halfWidthCeil; j++) {
      const jend = width - 1 - j
      const tmp = matrix[i][j]
      matrix[i][j] = matrix[jend][i];
      matrix[jend][i] = matrix[iend][jend]
      matrix[iend][jend] = matrix[j][iend]
      matrix[j][iend] = tmp
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Hash Table”: https://leetcode.com/tag/hash-table “String”: https://leetcode.com/tag/string Similar Questions: “Valid Anagram”: https://leetcode.com/problems/valid-anagram “Group Shifted Strings”: https://leetcode.com/problems/group-shifted-strings

49. Group Anagrams

Problem:

Given an array of strings, group anagrams together.

Example:

Input: ["eat", "tea", "tan", "ate", "nat", "bat"],
Output:
[
  ["ate","eat","tea"],
  ["nat","tan"],
  ["bat"]
]

Note:

• All inputs will be in lowercase.
• The order of your output does not matter.

Solution:

It’s all about hashing the words.

ONE

Sort each word to get the key.

/**
 * @param {string[]} strs
 * @return {string[][]}
 */
let groupAnagrams = function(strs) {
  let result = {};
  for (let i = 0; i < strs.length; i++) {
    const hash = strs[i].split('').sort().join('');
    result[hash] = result[hash] || []
    result[hash].push(strs[i])
  }
  return Object.values(result)
};

TWO

Use the product of prime numbers to generate unique keys.

const prime = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101]

/**
 * @param {string[]} strs
 * @return {string[][]}
 */
let groupAnagrams = function(strs) {
  const result = {};
  for (let i = 0; i < strs.length; i++) {
    const word = strs[i]
    let hash = 1
    for (let k = 0; k < word.length; k++) {
      hash *= prime[word.charCodeAt(k) - 97]
    }
    result[hash] = result[hash] || []
    result[hash].push(word)
  }
  return Object.values(result)
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Math”: https://leetcode.com/tag/math “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “Sqrt(x)”: https://leetcode.com/problems/sqrtx “Super Pow”: https://leetcode.com/problems/super-pow

50. Pow(x, n)

Problem:

Implement pow(x, n), which calculates x raised to the power n (xn).

Example 1:

Input: 2.00000, 10
Output: 1024.00000

Example 2:

Input: 2.10000, 3
Output: 9.26100

Example 3:

Input: 2.00000, -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

Note:

• -100.0 < x < 100.0
• n is a 32-bit signed integer, within the range [−231, 231 − 1]

Solution:

x^n = x^(n/2) * x^(n/2), if n is even
x^n = x^((n-1)/2) * x^((n-1)/2) * x, if n is odd

Corner cases:

• n == 0
• n < 0

Note here we can not use any bitwise operator, n = -2^31 might overflow.

/**
 * @param {number} x
 * @param {number} n
 * @return {number}
 */
let myPow = function(x, n) {
  if (n === 0) { return 1 }
  if (n === 1) { return x }
  if (n === -1) { return 1 / x }
  if (n % 2 === 0) {
    const res = myPow(x, n / 2)
    return res * res
  }
  const res = myPow(x, (n - 1) / 2)
  return x * res * res
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “N-Queens II”: https://leetcode.com/problems/n-queens-ii

51. N-Queens

Problem:

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

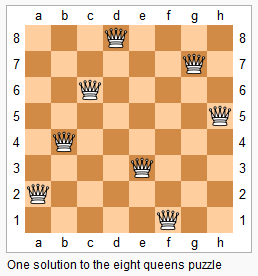
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

Solution:

Allocate a n-length array queens. Each item represents a queen coordinate on the borad. Let index i be the row index, and queens[i] be the column index (or vice versa).

Now use the permutation algorithm from 46. Permutations to generate all possible queen positions, then test for diagonal.

ONE

/**
 * @param {number} n
 * @return {string[][]}
 */
let solveNQueens = function(n) {
  const result = []
  const queens = [...new Array(n)].map((_, i) => i)
  _solveNQueens(queens, 0, result)
  return result
};

function _solveNQueens (queens, iStart, result) {
  if (iStart === queens.length) {
    for (let i = 0; i < queens.length; i += 1) {
      for (let j = i + 1; j < queens.length; j += 1) {
        if (Math.abs(i - j) === Math.abs(queens[i] - queens[j])) {
          return
        }
      }
    }
    return result.push(_genBoard(queens))
  }

  const start = queens[iStart]
  for (let i = iStart; i < queens.length; i++) {
    const next = queens[i]

    queens[iStart] = next
    queens[i] = start

    _solveNQueens(queens, iStart + 1, result)

    queens[iStart] = start
    queens[i] = next
  }
};

function _genBoard (queens) {
  const board = []
  for (let i = 0; i < queens.length; i++) {
    let row = ''
    for (let j = 0; j < queens.length; j++) {
      row += queens[i] === j ? 'Q' : '.'
    }
    board.push(row)
  }
  return board
};

This is slow because we test diagonal in the end. We can do a tree pruning by moving it right before diving into the next recursion.

TWO

/**
 * @param {number} n
 * @return {string[][]}
 */
let solveNQueens = function(n) {
  const result = []
  const queens = [...new Array(n)].map((_, i) => i)
  _solveNQueens(queens, 0, result)
  return result
};

function _solveNQueens (queens, iStart, result) {
  if (iStart === queens.length) {
    return result.push(_genBoard(queens))
  }

  const start = queens[iStart]
  for (let i = iStart; i < queens.length; i++) {
    const next = queens[i]

    queens[iStart] = next
    queens[i] = start

    if (_testDiagonal(queens, iStart)) {
      _solveNQueens(queens, iStart + 1, result)
    }

    queens[iStart] = start
    queens[i] = next
  }
};

function _testDiagonal(queens, iStart) {
  for (let i = 0; i < iStart; i++) {
    if (Math.abs(queens[iStart] - queens[i]) === iStart - i) {
      return false
    }
  }
  return true
};

function _genBoard (queens) {
  const board = []
  for (let i = 0; i < queens.length; i++) {
    let row = ''
    for (let j = 0; j < queens.length; j++) {
      row += queens[i] === j ? 'Q' : '.'
    }
    board.push(row)
  }
  return board
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “N-Queens”: https://leetcode.com/problems/n-queens

52. N-Queens II

Problem:

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example:

Input: 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown below.
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Solution:

Just modify 51. N-Queens.

/**
 * @param {number} n
 * @return {string[][]}
 */
let totalNQueens = function(n) {
  return _totalNQueens([...new Array(n)].map((_, i) => i), 0)
};

function _totalNQueens (queens, iStart, result) {
  if (iStart === queens.length) {
    return 1
  }

  let count = 0

  const start = queens[iStart]
  for (let i = iStart; i < queens.length; i++) {
    const next = queens[i]

    queens[iStart] = next
    queens[i] = start

    if (_testDiagonal(queens, iStart)) {
      count += _totalNQueens(queens, iStart + 1, result)
    }

    queens[iStart] = start
    queens[i] = next
  }

  return count
};

function _testDiagonal(queens, iStart) {
  for (let i = 0; i < iStart; i++) {
    if (Math.abs(queens[iStart] - queens[i]) === iStart - i) {
      return false
    }
  }
  return true
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Divide and Conquer”: https://leetcode.com/tag/divide-and-conquer “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “Best Time to Buy and Sell Stock”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock “Maximum Product Subarray”: https://leetcode.com/problems/maximum-product-subarray “Degree of an Array”: https://leetcode.com/problems/degree-of-an-array

53. Maximum Subarray

Problem:

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

Solution:

DP.

Define f(i) to be the largest sum of a contiguous subarray that ends with nums[i].

If f(i-1) is negative, then nums[i] must be greater than f(i-1) + nums[i].

f(0) = nums[0]
f(i) = max( f(i-1), 0 ) + nums[i]

Then return the largest one.

/**
 * @param {number[]} nums
 * @return {number}
 */
let maxSubArray = function(nums) {
  const len = nums.length
  if (len <= 0) { return 0 }
  const dp = [nums[0]]
  for (let i = 1; i < len; i++) {
    dp[i] = Math.max(dp[i-1], 0) + nums[i]
  }
  return Math.max(...dp)
};

We can also compress the dp array:

/**
 * @param {number[]} nums
 * @return {number}
 */
let maxSubArray = function(nums) {
  let dp = nums[0]
  let max = dp || 0
  for (let i = 1; i < nums.length; i++) {
    max = Math.max(max, dp = Math.max(dp, 0) + nums[i])
  }
  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Spiral Matrix II”: https://leetcode.com/problems/spiral-matrix-ii

54. Spiral Matrix

Problem:

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Solution:

Loop outside-in. Break each cycle into four stages. Note that the last two stages need at least two rows/columns.

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
let spiralOrder = function(matrix) {
  const result = []
  const height = matrix.length
  if (height <= 1) { return matrix[0] || result }
  const width = matrix[0].length
  if (width <= 0) { return result }

  const end = (Math.min(width, height) + 1) / 2 | 0
  for (let start = 0; start < end; start++) {
    const rowEnd = height - start - 1
    const colEnd = width - start - 1
    for (let col = start; col <= colEnd; col++) {
      result.push(matrix[start][col])
    }
    for (let row = start + 1; row <= rowEnd; row++) {
      result.push(matrix[row][colEnd])
    }
    if (rowEnd > start) {
      for (let col = colEnd - 1; col >= start ; col--) {
        result.push(matrix[rowEnd][col])
      }
    }
    if (colEnd > start) {
      for (let row = rowEnd - 1; row > start ; row--) {
        result.push(matrix[row][start])
      }
    }
  }
  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Greedy”: https://leetcode.com/tag/greedy Similar Questions: “Jump Game II”: https://leetcode.com/problems/jump-game-ii

55. Jump Game

Problem:

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

Example 1:

Input: [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

Input: [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum
             jump length is 0, which makes it impossible to reach the last index.

Solution:

ONE

See 45. Jump Game II. If the range does not expand at some point, we know it is stuck.

/**
 * @param {number[]} nums
 * @return {boolean}
 */
let canJump = function(nums) {
  for (let l = 0, r = 1; r < nums.length;) {
    let rNext = r
    for (let i = l; i < r; i++) {
      const rNextAtmp = i + nums[i] + 1
      if (rNextAtmp > rNext) {
        rNext = rNextAtmp
      }
    }
    if (rNext <= r) { return false }
    l = r
    r = rNext
  }
  return true
};

TWO

If we view it backward, and if the range of nums[n-2] covers nums[n-1], then we can safely make n-2 the new destination point, and so on.

If nums[0] can cover the last destination point, it is good.

/**
 * @param {number[]} nums
 * @return {boolean}
 */
let canJump = function(nums) {
  let des = nums.length - 1
  for (let i = des - 1; i > 0; i--) {
    if (nums[i] + i >= des) {
      des = i
    }
  }
  return nums[0] >= des
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Sort”: https://leetcode.com/tag/sort Similar Questions: “Insert Interval”: https://leetcode.com/problems/insert-interval “Meeting Rooms”: https://leetcode.com/problems/meeting-rooms “Meeting Rooms II”: https://leetcode.com/problems/meeting-rooms-ii “Teemo Attacking”: https://leetcode.com/problems/teemo-attacking “Add Bold Tag in String”: https://leetcode.com/problems/add-bold-tag-in-string “Range Module”: https://leetcode.com/problems/range-module “Employee Free Time”: https://leetcode.com/problems/employee-free-time “Partition Labels”: https://leetcode.com/problems/partition-labels

56. Merge Intervals

Problem:

Given a collection of intervals, merge all overlapping intervals.

Example 1:

Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].

Example 2:

Input: [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considerred overlapping.

Solution:

Sort then merge.

/**
 * Definition for an interval.
 * function Interval(start, end) {
 *     this.start = start;
 *     this.end = end;
 * }
 */
/**
 * @param {Interval[]} intervals
 * @return {Interval[]}
 */
let merge = function(intervals) {
  if (intervals.length <= 1) { return intervals }
  intervals.sort((a, b) => (a.start - b.start) || (a.end - b.end))
  let last = new Interval(intervals[0].start, intervals[0].end)
  const result = [last]
  for (let i = 1; i < intervals.length; i++) {
    const { start, end } = intervals[i]
    if (start > last.end) {
      last = new Interval(start, end)
      result.push(last)
    } else if (end > last.end) {
      last.end = end
    }
  }
  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Sort”: https://leetcode.com/tag/sort Similar Questions: “Merge Intervals”: https://leetcode.com/problems/merge-intervals “Range Module”: https://leetcode.com/problems/range-module

57. Insert Interval

Problem:

Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).

You may assume that the intervals were initially sorted according to their start times.

Example 1:

Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]

Example 2:

Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].

Solution:

The logic of the solution is pretty straight forward. Just need to carefully think through all the edge cases. It is better to choose readability over performance.

/**
 * Definition for an interval.
 * function Interval(start, end) {
 *     this.start = start;
 *     this.end = end;
 * }
 */
/**
 * @param {Interval[]} intervals
 * @param {Interval} newInterval
 * @return {Interval[]}
 */
let insert = function(intervals, newInterval) {
  const result = []
  const p = new Interval(newInterval.start, newInterval.end)
  for (let i = 0; i < intervals.length; i++) {
    const { start, end } = intervals[i]
    if (start > p.end) {
      break
    }

    if (end < p.start) {
      result.push(intervals[i])
      continue
    }

    if (start < p.start) {
      p.start = start
    }

    if (end > p.end) {
      p.end = end
    }
  }
  return [...result, p, ...intervals.slice(i)]
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “String”: https://leetcode.com/tag/string

58. Length of Last Word

Problem:

Given a string s consists of upper/lower-case alphabets and empty space characters ' ', return the length of last word in the string.

If the last word does not exist, return 0.

Note: A word is defined as a character sequence consists of non-space characters only.

Example:

Input: "Hello World"
Output: 5

Solution:

JavaScript specific solutions:

ONE

/**
 * @param {string} s
 * @return {number}
 */
let lengthOfLastWord = function(s) {
  return (/\w+$/.exec(s) || [''])[0].length
};

TWO

Super fast. split will guarantee that there is at least one item in the resulted array.

/**
 * @param {string} s
 * @return {number}
 */
let lengthOfLastWord = function(s) {
  return s.trim().split(' ').pop().length
};

THREE

General solution.

/**
 * @param {string} s
 * @return {number}
 */
let lengthOfLastWord = function(s) {
  let end = s.length - 1
  while (end >= 0 && s[end] === ' ') {
    end--
  }

  let start = end
  while (start >= 0 && s[start] !== ' ') {
    start--
  }

  return end - start
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Spiral Matrix”: https://leetcode.com/problems/spiral-matrix

59. Spiral Matrix II

Problem:

Given a positive integer n, generate a square matrix filled with elements from 1 to n2 in spiral order.

Example:

Input: 3
Output:
[
 [ 1, 2, 3 ],
 [ 8, 9, 4 ],
 [ 7, 6, 5 ]
]

Solution:

Straight-forward.

/**
 * @param {number} n
 * @return {number[][]}
 */
let generateMatrix = function(n) {
  const matrix = [...new Array(n)].map(() => [])
  const halfN = (n + 1) / 2 | 0
  let count = 1
  for (let start = 0; start < halfN; start++) {
    const end = n - start - 1
    for (let col = start; col <= end; col++) {
      matrix[start][col] = count++
    }
    for (let row = start + 1; row <= end; row++) {
      matrix[row][end] = count++
    }
    for (let col = end - 1; col >= start; col--) {
      matrix[end][col] = count++
    }
    for (let row = end - 1; row > start; row--) {
      matrix[row][start] = count++
    }
  }
  return matrix
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Math”: https://leetcode.com/tag/math “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Next Permutation”: https://leetcode.com/problems/next-permutation “Permutations”: https://leetcode.com/problems/permutations

60. Permutation Sequence

Problem:

The set [1,2,3,...,*n*] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, we get the following sequence for n = 3:

1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"

Given n and k, return the kth permutation sequence.

Note:

• Given n will be between 1 and 9 inclusive.
• Given k will be between 1 and n! inclusive.

Example 1:

Input: n = 3, k = 3
Output: "213"

Example 2:

Input: n = 4, k = 9
Output: "2314"

Solution:

The order of the sequence is fixed hence can be calculated. We can view the process as picking digits from a sorted set [1...n].

Each digit appears (n-1)! times in result[0]. And for a fixed result[0] each digit appears (n-2)! times in result[1]. So on.

We also need k-- to convert k into index so that k <= (n-1)! maps 0 (and get 1 from the set).

/**
 * @param {number} n
 * @param {number} k
 * @return {string}
 */
let getPermutation = function(n, k) {
  const digits = []
  let factorial = 1
  for (let i = 1; i <= n; i++) {
    digits.push(i)
    factorial *= i
  }

  k--

  let result = ''
  while (n > 0) {
    factorial /= n
    result += digits.splice(k / factorial | 0, 1)[0]
    k %= factorial
    n--
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Linked List”: https://leetcode.com/tag/linked-list “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Rotate Array”: https://leetcode.com/problems/rotate-array “Split Linked List in Parts”: https://leetcode.com/problems/split-linked-list-in-parts

61. Rotate List

Problem:

Given a linked list, rotate the list to the right by k places, where k is non-negative.

Example 1:

Input: 1->2->3->4->5->NULL, k = 2
Output: 4->5->1->2->3->NULL
Explanation:
rotate 1 steps to the right: 5->1->2->3->4->NULL
rotate 2 steps to the right: 4->5->1->2->3->NULL

Example 2:

Input: 0->1->2->NULL, k = 4
Output: 2->0->1->NULL
Explanation:
rotate 1 steps to the right: 2->0->1->NULL
rotate 2 steps to the right: 1->2->0->NULL
rotate 3 steps to the right: 0->1->2->NULL
rotate 4 steps to the right: 2->0->1->NULL

Solution:

Classic two-pointers chasing except the k could be larger than the length of this list.

We first attempt to locate the right pointer while also recording the length of the list.

If we hit the end of list and still do not have the right pointer, we know k is larger than the length.

Locate the right pointer again with k % len.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
let rotateRight = function(head, k) {
  if (head === null || k <= 0) { return head }

  let right = head
  let len = 0
  let kk = k
  while (right !== null && kk > 0) {
    right = right.next
    kk--
    len++
  }

  if (kk > 0) {
    right = head
    kk = k % len
    while (kk--) {
      right = right.next
    }
  }

  if (right !== null) {
    let left = head
    while (right.next !== null) {
      left = left.next
      right = right.next
    }
    right.next = head
    head = left.next
    left.next = null
  }

  return head
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “Unique Paths II”: https://leetcode.com/problems/unique-paths-ii “Minimum Path Sum”: https://leetcode.com/problems/minimum-path-sum “Dungeon Game”: https://leetcode.com/problems/dungeon-game

62. Unique Paths

Problem:

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

Solution:

DP.

Define f(i, j) to be the number of total unique paths from (0, 0) to (i, j).

f(i, 0) = 1
f(0, j) = 1
f(i, j) = f(i-1, j) + f(i, j-1)

Only two previous states are dependant. Use dynamic array to reduce memory allocation.

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
let uniquePaths = function(m, n) {
  const dp = new Array(m).fill(1)
  while (--n > 0) {
    for (let i = 1; i < m; i++) {
      dp[i] += dp[i-1]
    }
  }
  return dp[m-1] || 1
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “Unique Paths”: https://leetcode.com/problems/unique-paths “Dungeon Game”: https://leetcode.com/problems/dungeon-game “Cherry Pickup”: https://leetcode.com/problems/cherry-pickup

64. Minimum Path Sum

Problem:

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

Solution:

Define f(i, j) to be the min sum from (0, 0) to (i, j).

f(0, 0) = grid[0][0]
f(0, j) = f(0, j-1) + grid[0][j], j > 0
f(i, 0) = f(i-1, 0) + grid[i][0], i > 0
f(i, j) = min( f(i-1, j), f(i, j-1) ) + grid[i][j], j > 0 && i > 0

Only two previous states are dependant. Use dynamic array to reduce memory allocation.

/**
 * @param {number[][]} grid
 * @return {number}
 */
let minPathSum = function(grid) {
  const height = grid.length
  if (height <= 0) { return 0 }
  const width = grid[0].length
  if (width <= 0) { return 0 }

  const dp = new Array(width).fill(Infinity)
  dp[0] = 0
  for (let i = 0; i < height; i++) {
    dp[0] += grid[i][0]
    for (let j = 1; j < width; j++) {
      dp[j] = Math.min(dp[j], dp[j-1]) + grid[i][j]
    }
  }

  return dp[width-1] || 0
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Math”: https://leetcode.com/tag/math “String”: https://leetcode.com/tag/string Similar Questions: “String to Integer (atoi)”: https://leetcode.com/problems/string-to-integer-atoi

65. Valid Number

Problem:

Validate if a given string is numeric.

Some examples:
"0" => true
" 0.1 " => true
"abc" => false
"1 a" => false
"2e10" => true

Note: It is intended for the problem statement to be ambiguous. You should gather all requirements up front before implementing one.

Update (2015-02-10):
The signature of the C++ function had been updated. If you still see your function signature accepts a const char * argument, please click the reload button to reset your code definition.

Solution:

JavaScript specific solutions:

ONE

• Math.abs will first convert the argument to number.
• Math.abs(' ') === 0.

/**
 * @param {string} s
 * @return {boolean}
 */
let isNumber = function(s) {
  return !!s.trim() && Math.abs(s) >= 0
};

TWO

• isNaN will first convert the argument to number.
• isNaN(' ') === false.

/**
 * @param {string} s
 * @return {boolean}
 */
let isNumber = function(s) {
  return !!s.trim() && !isNaN(s)
};

THREE

General solution. Take a look at the ECMA Spec.

Similary, we can define our own syntax, which requires a few changes:

SignedDecimalLiteral::
  DecimalLiteral
  + DecimalLiteral
  - DecimalLiteral

DecimalLiteral::
  DecimalDigits . [DecimalDigits] [ExponentPart]
  . DecimalDigits [ExponentPart]
  DecimalDigits [ExponentPart]

DecimalDigits::
  DecimalDigit
  DecimalDigits DecimalDigit

DecimalDigit:: one of
  0123456789

ExponentPart::
  ExponentIndicator SignedInteger

ExponentIndicator::one of
  eE

SignedInteger::
  DecimalDigits
  + DecimalDigits
  - DecimalDigits

Now implement the parser. It is much easier now because we have a clear mental map of the syntax.

/**
 * @param {string} s
 * @return {boolean}
 */
let isNumber = function(s) {
  let start = 0
  while (s[start] === ' ') {
    start++
  }
  if (s[start] === '+' || s[start] === '-') {
    start++
  }
  let nextIndex = parseDecimalLiteral(s, start)
  while (s[nextIndex] === ' ') {
    nextIndex++
  }
  return nextIndex === s.length
}

/**
 * @param {string} s
 * @param {number} start - start index
 * @return {number} next index, -1 means error
 */
function parseDecimalLiteral (s, start) {
  let nextIndex = -1
  if (s[start] === '.') {
    nextIndex = parseDecimalDigits(s, start + 1)
    if (nextIndex === -1) { return -1 }
  } else {
    nextIndex = parseDecimalDigits(s, start)
    if (nextIndex === -1) { return -1 }

    if (s[nextIndex] === '.') {
      const optNextIndex = parseDecimalDigits(s, ++nextIndex)
      if (optNextIndex !== -1) {
        nextIndex = optNextIndex
      }
    }
  }

  const optNextIndex = parseExponentPart(s, nextIndex)
  return optNextIndex === -1 ? nextIndex : optNextIndex
}

/**
 * @param {string} s
 * @param {number} start - start index
 * @return {number} next index, -1 means error
 */
function parseDecimalDigits (s, start) {
  if (start === s.length) { return -1 }

  for (let i = start; i < s.length; i++) {
    const digit = s.charCodeAt(i) - 48
    if (!(digit >= 0 && digit <= 9)) {
      return i === start ? -1 : i
    }
  }
  return s.length
}

/**
 * @param {string} s
 * @param {number} start - start index
 * @return {number} next index, -1 means error
 */
function parseDecimalIntegerLiteral (s, start) {
  if (start === s.length) { return -1 }

  let nextIndex = start
  if (s[start] === '0') {
    nextIndex++
  }

  const digit = s.charCodeAt(nextIndex) - 48
  if (!(digit > 0 && digit <= 9)) {
    return nextIndex === start ? -1 : nextIndex
  }
  nextIndex++

  const optNextIndex = parseDecimalDigits (s, nextIndex)
  return optNextIndex === -1 ? nextIndex : optNextIndex
}

/**
 * @param {string} s
 * @param {number} start - start index
 * @return {number} next index, -1 means error
 */
function parseExponentPart (s, start) {
  if (s[start] !== 'e' && s[start] !== 'E') {
    return -1
  }

  let nextIndex = start + 1
  if (s[nextIndex] === '+' || s[nextIndex] === '-') {
    nextIndex++
  }

  return parseDecimalDigits(s, nextIndex)
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Math”: https://leetcode.com/tag/math Similar Questions: “Multiply Strings”: https://leetcode.com/problems/multiply-strings “Add Binary”: https://leetcode.com/problems/add-binary “Plus One Linked List”: https://leetcode.com/problems/plus-one-linked-list

66. Plus One

Problem:

Given a non-empty array of digits representing a non-negative integer, plus one to the integer.

The digits are stored such that the most significant digit is at the head of the list, and each element in the array contain a single digit.

You may assume the integer does not contain any leading zero, except the number 0 itself.

Example 1:

Input: [1,2,3]
Output: [1,2,4]
Explanation: The array represents the integer 123.

Example 2:

Input: [4,3,2,1]
Output: [4,3,2,2]
Explanation: The array represents the integer 4321.

Solution:

ONE

JavaScript specific solution. Note that unshift is much slower that expanding.

/**
 * @param {number[]} digits
 * @return {number[]}
 */
let plusOne = function(digits) {
  for (let i = digits.length - 1; i >= 0; i--) {
    if (digits[i] < 9) {
      digits[i]++
      return digits
    }
    digits[i] = 0
  }
  return [1, ...digits]
};

TWO

General solution.

/**
 * @param {number[]} digits
 * @return {number[]}
 */
let plusOne = function(digits) {
  for (let i = digits.length - 1; i >= 0; i--) {
    if (digits[i] < 9) {
      digits[i]++
      return digits
    }
    digits[i] = 0
  }

  for (let i = digits.length; i > 0; i--) {
    digits[i] = digits[i-1]
  }
  digits[0] = 1

  return digits
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “String”: https://leetcode.com/tag/string

68. Text Justification

Problem:

Given an array of words and a width maxWidth, format the text such that each line has exactly maxWidth characters and is fully (left and right) justified.

You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces ' ' when necessary so that each line has exactly maxWidth characters.

Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line do not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.

For the last line of text, it should be left justified and no extra space is inserted between words.

Note:

• A word is defined as a character sequence consisting of non-space characters only.
• Each word’s length is guaranteed to be greater than 0 and not exceed maxWidth.
• The input array words contains at least one word.

Example 1:

Input:
words = ["This", "is", "an", "example", "of", "text", "justification."]
maxWidth = 16
Output:
[
   "This    is    an",
   "example  of text",
   "justification.  "
]

Example 2:

Input:
words = ["What","must","be","acknowledgment","shall","be"]
maxWidth = 16
Output:
[
  "What   must   be",
  "acknowledgment  ",
  "shall be        "
]
Explanation: Note that the last line is "shall be    " instead of "shall     be",
             because the last line must be left-justified instead of fully-justified.
             Note that the second line is also left-justified becase it contains only one word.

Example 3:

Input:
words = ["Science","is","what","we","understand","well","enough","to","explain",
         "to","a","computer.","Art","is","everything","else","we","do"]
maxWidth = 20
Output:
[
  "Science  is  what we",
  "understand      well",
  "enough to explain to",
  "a  computer.  Art is",
  "everything  else  we",
  "do                  "
]

Solution:

• Count the current line width (plus 1 space between each two words).
• When a line is full:
  • If there is only one word, pad spaces at the end.
  • Otherwise calculate the gap length using Math.ceil.
• Handle the last line.

/**
 * @param {string[]} words
 * @param {number} maxWidth
 * @return {string[]}
 */
let fullJustify = function(words, maxWidth) {
  let start = 0
  let end = 1
  let lineLen = words[start].length
  const result = []

  while (end < words.length) {
    const newLen = words[end].length + 1 + lineLen
    if (newLen <= maxWidth) {
      lineLen = newLen
    } else {
      let line = ''
      let nWords = end - start
      if (nWords === 1) {
        line = words[start].padEnd(maxWidth)
      } else {
        let nSpaces = maxWidth - (lineLen - (nWords - 1))
        for (let i = start; i < end; i++) {
          const gap = Math.ceil(nSpaces / (end - i - 1))
          line += words[i] + ' '.repeat(gap)
          nSpaces -= gap
        }
      }
      result.push(line)
      start = end
      lineLen = words[start].length
    }
    end++
  }

  let lastline = words[start]
  for (let i = start + 1; i < end; i++) {
    lastline += ' ' + words[i]
  }
  result.push(lastline.padEnd(maxWidth))

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Math”: https://leetcode.com/tag/math “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “Pow(x, n)”: https://leetcode.com/problems/powx-n “Valid Perfect Square”: https://leetcode.com/problems/valid-perfect-square

69. Sqrt(x)

Problem:

Implement int sqrt(int x).

Compute and return the square root of x, where x is guaranteed to be a non-negative integer.

Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.

Example 1:

Input: 4
Output: 2

Example 2:

Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since
             the decimal part is truncated, 2 is returned.

Solution:

Binary Search. The square root of x is within [0…(x+1)/2].

/**
 * @param {number} x
 * @return {number}
 */
let mySqrt = function(x) {
  let max = Math.round(x / 2)
  let min = 0
  while (min <= max) {
    const mid = Math.floor((min + max) / 2)
    const diff = mid * mid - x
    if (diff > 0) {
      max = mid - 1
    } else if (diff < 0) {
      min = mid + 1
    } else {
      return mid
    }
  }
  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “String”: https://leetcode.com/tag/string “Stack”: https://leetcode.com/tag/stack

71. Simplify Path

Problem:

Given an absolute path for a file (Unix-style), simplify it.

For example,
path = "/home/", => "/home"
path = "/a/./b/../../c/", => "/c"

Corner Cases:

• Did you consider the case where path = "/../"?
  In this case, you should return "/".
• Another corner case is the path might contain multiple slashes '/' together, such as "/home//foo/".
  In this case, you should ignore redundant slashes and return "/home/foo".

Solution:

Use stack to handle /../.

ONE

RegExp matching.

/**
 * @param {string} path
 * @return {string}
 */
let simplifyPath = function(path) {
  return '/' + (path.match(/[^\/]+/g) || [])
    .reduce((stack, p) => {
      if (p === '..') {
        stack.pop()
      } else if (p !== '.') {
        stack.push(p)
      }
      return stack
    }, [])
    .join('/')
};

TWO

Direct search.

/**
 * @param {string} path
 * @return {string}
 */
let simplifyPath = function(path) {
  const len = path.length
  const stack = []
  let e = 0
  while (e < len) {
    while (e < len && path[e] === '/') {
      e++
    }
    const s = e
    while (e < len && path[e] !== '/') {
      e++
    }
    if (s < e) {
      const p = path.slice(s, e)
      if (p === '..') {
        stack.pop()
      } else if (p !== '.') {
        stack.push(p)
      }
    }
  }
  return '/' + stack.join('/')
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “String”: https://leetcode.com/tag/string “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “One Edit Distance”: https://leetcode.com/problems/one-edit-distance “Delete Operation for Two Strings”: https://leetcode.com/problems/delete-operation-for-two-strings “Minimum ASCII Delete Sum for Two Strings”: https://leetcode.com/problems/minimum-ascii-delete-sum-for-two-strings

72. Edit Distance

Problem:

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

Solution:

DP.

Define f(i, j) to be the min edit distance from word1[0...i) to word2[0...j).

f(0, 0) = 0
f(0, j) = f(0, j-1) + 1 // can only insert
f(i, 0) = f(i-1, 0) + 1 // can only delete
f(i, j) = min(
  f(i, j-1) + 1 // insert
  f(i-1, j) + 1 // delete
  f(i-1, j-1) + (word1[i-1] !== word2[j-1] ? 1 : 0) // replace or do nothing
)

/**
 * @param {string} word1
 * @param {string} word2
 * @return {number}
 */
let minDistance = function(word1, word2) {
  const len1 = word1.length
  const len2 = word2.length

  if(len1 <= 0 || len2 <= 0) {
    return len1 + len2
  }

  const dp = []

  for (let i = 0; i <= len1; i++) {
    dp[i] = [i]
  }

  for (let j = 0; j <= len2; j++) {
    dp[0][j] = j
  }

  for (let i = 1; i <= len1; i++) {
    for (let j = 1; j <= len2; j++) {
      dp[i][j] = Math.min(
        dp[i][j-1] + 1,
        dp[i-1][j] + 1,
        dp[i-1][j-1] + (word1[i-1] === word2[j-1] ? 0 : 1)
      )
    }
  }

  return dp[len1][len2]
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Game of Life”: https://leetcode.com/problems/game-of-life

73. Set Matrix Zeroes

Problem:

Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in-place.

Example 1:

Input:
[
  [1,1,1],
  [1,0,1],
  [1,1,1]
]
Output:
[
  [1,0,1],
  [0,0,0],
  [1,0,1]
]

Example 2:

Input:
[
  [0,1,2,0],
  [3,4,5,2],
  [1,3,1,5]
]
Output:
[
  [0,0,0,0],
  [0,4,5,0],
  [0,3,1,0]
]

Follow up:

• A straight forward solution using O(m**n) space is probably a bad idea.
• A simple improvement uses O(m + n) space, but still not the best solution.
• Could you devise a constant space solution?

Solution:

• O(m**n) space solution: Copy a new matrix.
• O(m + n) space solution: Use extra arrays to store rows and columns that need to be set 0.
• Constant space solutions:

ONE

Instead of allocating extra arrays. Just use the first row and column.

First scan through the first row and column to see if they need be set 0. If so, mark and do it in the end.

Now scan the matrix and set 0 to the first row and column whenever a 0 is met.

Walk the matrix again and set 0 according to the first row and column.

Finally set the first row and column to 0 if needed.

/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
let setZeroes = function(matrix) {
  const height = matrix.length
  if (height <= 0) { return }
  const width = matrix[0].length
  if (width <= 0) { return }

  const shouldClearFirstRow = matrix[0].some(x => x === 0)
  const shouldClearFirstCol = matrix.some(row => row[0] === 0)

  for (let i = 1; i < height; i++) {
    for (let j = 1; j < width; j++) {
      if (matrix[i][j] === 0) {
        matrix[i][0] = 0
        matrix[0][j] = 0
      }
    }
  }

  for (let i = 1; i < height; i++) {
    if (matrix[i][0] === 0) {
      matrix[i].fill(0)
    }
  }

  for (let j = 1; j < width; j++) {
    if (matrix[0][j] === 0) {
      for (let i = 1; i < height; i++) {
        matrix[i][j] = 0
      }
    }
  }

  if (shouldClearFirstRow) {
    matrix[0].fill(0)
  }

  if (shouldClearFirstCol) {
    for (let i = 0; i < height; i++) {
      matrix[i][0] = 0
    }
  }
};

TWO

Use NaN to mark cells that need to be set 0.

Still constant space just a bit slower due to repeatedly setting overlapping NaNs.

/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
let setZeroes = function(matrix) {
  const height = matrix.length
  if (height <= 0) { return }
  const width = matrix[0].length
  if (width <= 0) { return }

  for (let i = 0; i < height; i++) {
    for (let j = 0; j < width; j++) {
      if (matrix[i][j] !== 0) { continue }

      for (let jj = 0; jj < width; jj++) {
        if (matrix[i][jj] !== 0) {
          matrix[i][jj] = NaN
        }
      }

      for (let ii = 0; ii < height; ii++) {
        if (matrix[ii][j] !== 0) {
          matrix[ii][j] = NaN
        }
      }
    }
  }

  for (let i = 0; i < height; i++) {
    for (let j = 0; j < width; j++) {
      if (isNaN(matrix[i][j])) {
        matrix[i][j] = 0
      }
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “Search a 2D Matrix II”: https://leetcode.com/problems/search-a-2d-matrix-ii

74. Search a 2D Matrix

Problem:

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
Output: true

Example 2:

Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
Output: false

Solution:

ONE

Search from top-left to bottom-right. O(n).

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
let searchMatrix = function(matrix, target) {
  const height = matrix.length
  if (height <= 0) { return false }
  const width = matrix[0].length
  if (width <= 0) { return false }

  let i = 0
  let j = width - 1
  while (i < height && j >= 0) {
    const diff = matrix[i][j] - target
    if (diff > 0) {
      j--
    } else if (diff < 0) {
      i++
    } else {
      return true
    }
  }

  return false
};

TWO

Binary search. O(logn).

View the matrix as an sorted array that is cut into n slices.

Take the algorithm from 35. Search Insert Position.

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
let searchMatrix = function(matrix, target) {
  const height = matrix.length
  if (height <= 0) { return false }
  const width = matrix[0].length
  if (width <= 0) { return false }

  let s = 0
  let e = width * height - 1
  while (s <= e) {
    const mid = Math.floor((s + e) / 2)
    const diff = matrix[Math.floor(mid / width)][mid % width] - target
    if (diff < 0) {
      s = mid + 1
    } else if (diff > 0) {
      e = mid - 1
    } else {
      return true
    }
  }

  return false
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers “Sort”: https://leetcode.com/tag/sort Similar Questions: “Sort List”: https://leetcode.com/problems/sort-list “Wiggle Sort”: https://leetcode.com/problems/wiggle-sort “Wiggle Sort II”: https://leetcode.com/problems/wiggle-sort-ii

75. Sort Colors

Problem:

Given an array with n objects colored red, white or blue, sort them in-placeso that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note: You are not suppose to use the library’s sort function for this problem.

Example:

Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

Follow up:

• A rather straight forward solution is a two-pass algorithm using counting sort.
  First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.
• Could you come up with a one-pass algorithm using only constant space?

Solution:

One-pass algorithm.

Take the idea of the partition algorithm from quick sort. Use 1 as pivot.

Count the number of sorted 0s and 2s so that we know where to swap.

/**
 * @param {number[]} nums
 * @return {void} Do not return anything, modify nums in-place instead.
 */
let sortColors = function(nums) {
  const len = nums.length
  let zeroEnd = 0
  let twoStart = len - 1
  let i = 0
  while (i <= twoStart) {
    if (nums[i] === 0 && i !== zeroEnd) {
      const t = nums[i]
      nums[i] = nums[zeroEnd]
      nums[zeroEnd] = t
      zeroEnd++
    } else if (nums[i] === 2 && i !== twoStart) {
      const t = nums[i]
      nums[i] = nums[twoStart]
      nums[twoStart] = t
      twoStart--
    } else {
      i++
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Combination Sum”: https://leetcode.com/problems/combination-sum “Permutations”: https://leetcode.com/problems/permutations

77. Combinations

Problem:

Given two integers n and k, return all possible combinations of k numbers out of 1 … n.

Example:

Input: n = 4, k = 2
Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

Solution:

Basic DFS + Backtracking.

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
let combine = function(n, k) {
  const result = []
  _combine(1, [], n, k, result)
  return result
};

function _combine (cur, path, n, k, result) {
  if (path.length === k) {
    return result.push(path.slice())
  }

  while (cur <= n) {
    path.push(cur)
    _combine(++cur, path, n, k, result)
    path.pop()
  }
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Backtracking”: https://leetcode.com/tag/backtracking “Bit Manipulation”: https://leetcode.com/tag/bit-manipulation Similar Questions: “Subsets II”: https://leetcode.com/problems/subsets-ii “Generalized Abbreviation”: https://leetcode.com/problems/generalized-abbreviation “Letter Case Permutation”: https://leetcode.com/problems/letter-case-permutation

78. Subsets

Problem:

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

Solution:

ONE

BFS.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let subsets = function(nums) {
  return nums.reduce((result, num) => result.concat(result.map(r => [...r, num])), [[]])
};

Or more imperative. Loop backward to avoid crossing the boundary.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let subsets = function(nums) {
  const result = [[]]
  for (let i = nums.length - 1; i >= 0; i--) {
    for (let j = result.length - 1; j >= 0; j--) {
      result.push([nums[i], ...result[j]])
    }
  }
  return result
};

TWO

DFS + Backtracking.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let subsets = function(nums) {
  const result = []
  _subsets(nums, 0, [], result)
  return result
};

function _subsets(nums, start, path, result) {
  result.push(path.slice())
  while (start < nums.length) {
    path.push(nums[start])
    _subsets(nums, ++start, path, result)
    path.pop()
  }
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Word Search II”: https://leetcode.com/problems/word-search-ii

79. Word Search

Problem:

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

Solution:

DFS + Backtracking. Replace the cell with NaN before proceeding to the next level and restore when backtracking.

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
let exist = function(board, word) {
  const height = board.length
  if (height <= 0) { return false }
  const width = board[0].length
  if (width <= 0) { return false }

  for (let row = 0; row < height; row++) {
    for (let col = 0; col < width; col++) {
      if (board[row][col] === word[0] &&
          _exist(board, word, 0, [[-1, 0], [1, 0], [0, -1], [0, 1]], row, col)
      ) {
        return true
      }
    }
  }

  return false
};

function _exist (board, word, iWord, directions, row, col) {
  if (iWord === word.length) {
    return true
  }

  if (!board[row] || word[iWord] !== board[row][col]) {
    return false
  }

  const cell = board[row][col]
  board[row][col] = NaN

  for (let i = directions.length - 1; i >= 0; i--) {
    if (_exist(board, word, iWord+1, directions, row+directions[i][0], col+directions[i][1])) {
      return true
    }
  }

  board[row][col] = cell

  return false
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Remove Duplicates from Sorted Array”: https://leetcode.com/problems/remove-duplicates-from-sorted-array

80. Remove Duplicates from Sorted Array II

Problem:

Given a sorted array nums, remove the duplicates in-place such that duplicates appeared at most twice and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Example 1:

Given nums = [1,1,1,2,2,3],

Your function should return length = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.

It doesn't matter what you leave beyond the returned length.

Example 2:

Given nums = [0,0,1,1,1,1,2,3,3],

Your function should return length = 7, with the first seven elements of nums being modified to 0, 0, 1, 1, 2, 3 and 3 respectively.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy)
int len = removeDuplicates(nums);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

Solution:

Similar to 26. Remove Duplicates from Sorted Array.

/**
 * @param {number[]} nums
 * @return {number}
 */
let removeDuplicates = function(nums) {
  let len = 0
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] !== nums[len-2]) {
      nums[len++] = nums[i]
    }
  }
  return len
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Binary Search”: https://leetcode.com/tag/binary-search Similar Questions: “Search in Rotated Sorted Array”: https://leetcode.com/problems/search-in-rotated-sorted-array

81. Search in Rotated Sorted Array II

Problem:

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,0,1,2,2,5,6] might become [2,5,6,0,0,1,2]).

You are given a target value to search. If found in the array return true, otherwise return false.

Example 1:

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2:

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Follow up:

• This is a follow up problem to Search in Rotated Sorted Array, where nums may contain duplicates.
• Would this affect the run-time complexity? How and why?

Solution:

See 33. Search in Rotated Sorted Array. The code is basically the same. Except with duplicates we can not tell which way to jump when pivot == nums[e]. The only thing we can do is to ditch nums[e]. SO worst case O(*n*).

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {boolean}
 */
let search = function(nums, target) {
  let s = 0
  let e = nums.length - 1

  while (s <= e) {
    const p = (e + s) / 2 | 0
    const pivot = nums[p]

    if (target === pivot) {
      return true
    }

    if (pivot < nums[e]) {
      if (target > nums[p] && target <= nums[e]) {
        s = p + 1
      } else {
        e = p - 1
      }
    } else if (pivot > nums[e]) {
      if (target < nums[p] && target >= nums[s]) {
        e = p - 1
      } else {
        s = p + 1
      }
    } else {
      e--
    }
  }

  return false
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Linked List”: https://leetcode.com/tag/linked-list Similar Questions: “Remove Duplicates from Sorted List”: https://leetcode.com/problems/remove-duplicates-from-sorted-list

82. Remove Duplicates from Sorted List II

Problem:

Given a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list.

Example 1:

Input: 1->2->3->3->4->4->5
Output: 1->2->5

Example 2:

Input: 1->1->1->2->3
Output: 2->3

Solution:

p1 points to the current node. p points to the node before p1 so that we can ditch p1 if needed.

The list is sorted so we only need dupVal to keep the latest duplicate value.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
let deleteDuplicates = function(head) {
  if (!head) { return null }
  const prehead = { next: head }

  let p = prehead
  let dupVal = NaN

  for (let p1 = head; p1; p1 = p1.next) {
    if (p1.val === dupVal) {
      p.next = p1.next
    } else if (p1.next && p1.val === p1.next.val) {
      p.next = p1.next
      dupVal = p1.val
    } else {
      p = p1
    }
  }

  return prehead.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Linked List”: https://leetcode.com/tag/linked-list Similar Questions: “Remove Duplicates from Sorted List II”: https://leetcode.com/problems/remove-duplicates-from-sorted-list-ii

83. Remove Duplicates from Sorted List

Problem:

Given a sorted linked list, delete all duplicates such that each element appear only once.

Example 1:

Input: 1->1->2
Output: 1->2

Example 2:

Input: 1->1->2->3->3
Output: 1->2->3

Solution:

ONE

Just like 82. Remove Duplicates from Sorted List II except keeping the first duplicate node.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
let deleteDuplicates = function(head) {
  if (!head) { return null }
  const prehead = { next: head }

  let p = prehead
  let dupVal = NaN

  for (let p1 = head; p1; p1 = p1.next) {
    if (p1.val === dupVal) {
      p.next = p1.next
    } else {
      if (p1.next && p1.val === p1.next.val) {
        dupVal = p1.val
      }
      p = p1
    }
  }

  return prehead.next
};

TWO

Just compare the next node. This is way more faster.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
let deleteDuplicates = function(head) {
  if (!head) { return null }

  let p = head
  while (p) {
    if (p.next && p.val === p.next.val) {
      p.next = p.next.next
    } else {
      p = p.next
    }
  }

  return head
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Stack”: https://leetcode.com/tag/stack Similar Questions: “Maximal Rectangle”: https://leetcode.com/problems/maximal-rectangle

84. Largest Rectangle in Histogram

Problem:

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

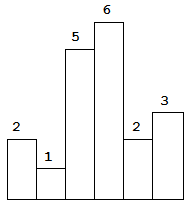
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

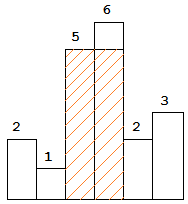
The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3]
Output: 10

Solution:

The height of a rectangle is determined by the lowest bar inside of it. So the core idea is, for each bar, assume it is the lowest bar and see how far it can expand. Then we have len(heights) rectangles. Return the max area.

For a bar b whose height is h, find the closest bar b1 on the left that is lower than h, and b2 on the right. The area of the rectangle is h * (i2 - i1 - 1).

Notice that if we just loop the bars from left to right, b1 and b2 of each bar may overlap.

Observe how i1 and i2 changes depending on the height.

To reduce O(n^2) to O(n), we use a stack to store incremental bs. Because b1 and b2 are both lower than b, whenever we reach a bar that is lower than the top of the stack, we know it’s a b2. So stack top is a b. Second top is a b1. Keep popping the b to calculate areas until b2 is no longer lower than stack top.

/**
 * @param {number[]} heights
 * @return {number}
 */
let largestRectangleArea = function(heights) {
  const stack = [-1]
  let max = 0
  for (let i2 = 0; i2 <= heights.length; i2++) {
    while ((heights[i2] || 0) < heights[stack[stack.length-1]]) {
      const i = stack.pop()
      const i1 = stack[stack.length-1]
      max = Math.max(max, heights[i] * (i2 - i1 - 1))
    }
    stack.push(i2)
  }
  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Hash Table”: https://leetcode.com/tag/hash-table “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming “Stack”: https://leetcode.com/tag/stack Similar Questions: “Largest Rectangle in Histogram”: https://leetcode.com/problems/largest-rectangle-in-histogram “Maximal Square”: https://leetcode.com/problems/maximal-square

85. Maximal Rectangle

Problem:

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.

Example:

Input:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
Output: 6

Solution:

ONE

View every row as a base line then we just have to solve height(matrix) times the problem of 84. Largest Rectangle in Histogram.

/**
 * @param {character[][]} matrix
 * @return {number}
 */
let maximalRectangle = function(matrix) {
  const height = matrix.length
  if (height <= 0) { return 0 }
  const width = matrix[0].length
  if (width <= 0) { return 0 }

  const heights = []
  let max = 0
  for (let row = 0; row < height; row++) {
    for (let col = 0; col < width; col++) {
      heights[col] = ((heights[col] || 0) + 1) * matrix[row][col]
    }
    max = Math.max(max, largestRectangleArea(heights))
  }

  return max
};

/**
 * @param {number[]} heights
 * @return {number}
 */
function largestRectangleArea (heights) {
  const stack = [-1]
  let max = 0
  for (let i2 = 0; i2 <= heights.length; i2++) {
    while ((heights[i2] || 0) < heights[stack[stack.length-1]]) {
      const i = stack.pop()
      const i1 = stack[stack.length-1]
      max = Math.max(max, heights[i] * (i2 - i1 - 1))
    }
    stack.push(i2)
  }
  return max
};

TWO

Same idea as above. Use DP to cache accumulated states.

Pick a pivot point (row, col) and assume it is on the base line. The adjoining 1s above (row, col) makes up the height of the rectangle. The width of the rectangle is determined by how many ajoining bars are taller than the pivot bar.

So for the rectangle whose bottom pivot is (row, col):

• Define area(row, col) to be the area.
• Define height(row, col) to be the height.
• Define left(row, col) to be the col value of the bottom-left corner.
• Define right(row, col) to be the col value of the bottom-right corner.

Also:

• Define conLeft(row, col) to be the col value of the leftmost cell of the consecutive 1s on the left of (row, col).
• Define conRight(row, col) to be the col value of the rightmost cell of the consecutive 1s on the right of (row, col).

With conLeft and conRight we can know if the rectangle on (row, col) shrinks comparing to (row-1, col).

if matrix[row][col] == 1
  height(row, col) = height(row-1, col) + 1

  // see how long this horizontal line can get
  conLeft(row, col) = conLeft(row, col-1)
  conRight(row, col) = conRight(row, col+1)

  // width can only be shorter
  left(row, col) = max( left(row-1, col), conLeft(row, col) )
  right(row, col) = min( right(row-1, col), conRight(row, col) )

if matrix[row][col] == 0
  height(row, col) = 0
  conLeft(row, col) = col + 1
  conRight(row, col) = col - 1
  left(row, col) = 0 // back to leftmost position
  right(row, col) = matrix.width // back to rightmost position

area(row, col) = (right(row, col) - left(row, col) + 1) * height(row, col)

We only need to keep the last state. Use dynamic arrays to reduce space complexity.

/**
 * @param {character[][]} matrix
 * @return {number}
 */
let maximalRectangle = function(matrix) {
  const height = matrix.length
  if (height <= 0) { return 0 }
  const width = matrix[0].length
  if (width <= 0) { return 0 }

  const heights = new Array(width).fill(0)
  const lefts = new Array(width).fill(0)
  const rights = new Array(width).fill(width)

  let max = 0

  for (let row = 0; row < height; row++) {
    let conLeft = 0
    let conRight = width - 1
    for (let col = 0; col < width; col++) {
      if (matrix[row][col] === '1') {
        heights[col] = heights[col] + 1
        lefts[col] = Math.max(lefts[col], conLeft)
      } else {
        heights[col] = 0
        lefts[col] = 0
        conLeft = col + 1
      }
    }

    for (let col = width - 1; col >= 0; col--) {
      if (matrix[row][col] === '1') {
        rights[col] = Math.min(rights[col], conRight)
      } else {
        rights[col] = width
        conRight = col - 1
      }
    }

    for (let col = 0; col < width; col++) {
      max = Math.max(max, (rights[col] - lefts[col] + 1) * heights[col])
    }
  }

  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Linked List”: https://leetcode.com/tag/linked-list “Two Pointers”: https://leetcode.com/tag/two-pointers

86. Partition List

Problem:

Given a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.

You should preserve the original relative order of the nodes in each of the two partitions.

Example:

Input: head = 1->4->3->2->5->2, x = 3
Output: 1->2->2->4->3->5

Solution:

Take the second part out as a new list and connect it back.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} x
 * @return {ListNode}
 */
let partition = function(head, x) {
  const prehead1 = { next: head }
  let p1 = prehead1
  let ptail1 = prehead1

  const prehead2 = { next: null }
  let p2 = prehead2

  while (p1) {
    const next = p1.next
    if (next && next.val >= x) {
      p1.next = next.next
      p2.next = next
      p2 = next
    } else {
      ptail1 = p1
      p1 = p1.next
    }
  }

  p2.next = null
  ptail1.next = prehead2.next

  return prehead1.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Two Pointers”: https://leetcode.com/tag/two-pointers Similar Questions: “Merge Two Sorted Lists”: https://leetcode.com/problems/merge-two-sorted-lists

88. Merge Sorted Array

Problem:

Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.

Note:

• The number of elements initialized in nums1 and nums2 are m and n respectively.
• You may assume that nums1 has enough space (size that is greater or equal to m + n) to hold additional elements from nums2.

Example:

Input:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

Output: [1,2,2,3,5,6]

Solution:

Loop backward and keep picking the larger one. nums1 is guaranteed longer than nums2 so just use n as boundary.

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void} Do not return anything, modify nums1 in-place instead.
 */
let merge = function(nums1, m, nums2, n) {
  let len = (m--) + (n--)
  while (n >= 0) {
    nums1[--len] = nums1[m] >= nums2[n] ? nums1[m--] : nums2[n--]
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “1-bit and 2-bit Characters”: https://leetcode.com/problems/1-bit-and-2-bit-characters

89. Gray Code

Problem:

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

Example 1:

Input: 2
Output: [0,1,3,2]
Explanation:
00 - 0
01 - 1
11 - 3
10 - 2

For a given n, a gray code sequence may not be uniquely defined.
For example, [0,2,3,1] is also a valid gray code sequence.

00 - 0
10 - 2
11 - 3
01 - 1

Example 2:

Input: 0
Output: [0]
Explanation: We define the gray code sequence to begin with 0.
             A gray code sequence of n has size = 2n, which for n = 0 the size is 20 = 1.
             Therefore, for n = 0 the gray code sequence is [0].

Solution:

0: [  0                                   ]
1: [  0,   1                              ]
2: [ 00,  01,  11,  10                    ]
3: [000, 001, 011, 010, 110, 111, 101, 100]

The pattern is self-evident. Reverse the result set and prepend ‘1’ to each item.

Use bitwise shift to speed up the calculation. It is unlikely to overflow since the result set is exponential.

/**
 * @param {number} n
 * @return {number[]}
 */
let grayCode = function(n) {
  const result = [0]
  for (let level = 0; level < n; level++) {
    const prefix = 1 << level
    for (let i = result.length - 1; i >= 0; i--) {
      result.push(result[i] + prefix)
    }
  }
  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “Subsets”: https://leetcode.com/problems/subsets

90. Subsets II

Problem:

Given a collection of integers that might contain duplicates, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

Input: [1,2,2]
Output:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

Solution:

See 78. Subsets. Except:

1. Sort input to group duplicates.
2. Only consider each duplicate once, that is, when it is at the first slot.

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let subsetsWithDup = function(nums) {
  const result = []
  _subsetsWithDup(nums.sort(), 0, [], result)
  return result
};

function _subsetsWithDup(nums, start, path, result) {
  result.push(path.slice())
  for (let i = start; i < nums.length; i++) {
    if(i > start && nums[i] === nums[i-1]) {
      continue
    }
    path.push(nums[i])
    _subsetsWithDup(nums, i + 1, path, result)
    path.pop()
  }
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “String”: https://leetcode.com/tag/string “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “Decode Ways II”: https://leetcode.com/problems/decode-ways-ii

91. Decode Ways

Problem:

A message containing letters from A-Z is being encoded to numbers using the following mapping:

'A' -> 1
'B' -> 2
...
'Z' -> 26

Given a non-empty string containing only digits, determine the total number of ways to decode it.

Example 1:

Input: "12"
Output: 2
Explanation: It could be decoded as "AB" (1 2) or "L" (12).

Example 2:

Input: "226"
Output: 3
Explanation: It could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).

Solution:

Define f(i) to be the number of ways to decode s[0...i].

Note that there could be '0'.

f(0) = 1, if s[i] !== '0'
f(i) = 0, if s.length <= 0 || s[i] === '0'
f(i) = f(i-1), if i > 0 && s[i] !== '0'
       +
       f(i-2), if i > 0 && s[i-1] !== '0' && s[i-1] * 10 + s[i] <= 26

Only need to store the last two states. Init f(-1) = 1 for easy calculation.

/**
 * @param {string} s
 * @return {number}
 */
let numDecodings = function(s) {
  let dp = s[0] > 0 ? 1 : 0
  let dp_1 = dp
  let dp_2 = 1

  for (let i = 1; i < s.length; i++) {
    dp = 0
    if (s[i] !== '0') {
      dp += dp_1
    }
    if (s[i-1] !== '0' && s[i-1] + s[i] <= 26) {
      dp += dp_2
    }
    dp_2 = dp_1
    dp_1 = dp
  }

  return dp
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Linked List”: https://leetcode.com/tag/linked-list Similar Questions: “Reverse Linked List”: https://leetcode.com/problems/reverse-linked-list

92. Reverse Linked List II

Problem:

Reverse a linked list from position m to n. Do it in one-pass.

**Note:**1 ≤ m ≤ n ≤ length of list.

Example:

Input: 1->2->3->4->5->NULL, m = 2, n = 4
Output: 1->4->3->2->5->NULL

Solution:

Break the list into 3 parts.

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} m
 * @param {number} n
 * @return {ListNode}
 */
let reverseBetween = function(head, m, n) {
  if (m === n) { return head }

  const prehead = { next: head }
  n = n - m

  let l1tail = prehead
  while (--m > 0) {
    l1tail = l1tail.next
  }

  let l2prehead = l1tail
  let l2head = l2prehead.next
  let l2tail = l2head
  while (n-- > 0) {
    const next = l2head.next
    l2head.next = l2prehead
    l2prehead = l2head
    l2head = next
  }

  l2tail.next = l2head.next // l3head
  l2head.next = l2prehead
  l1tail.next = l2head

  return prehead.next
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “String”: https://leetcode.com/tag/string “Backtracking”: https://leetcode.com/tag/backtracking Similar Questions: “IP to CIDR”: https://leetcode.com/problems/ip-to-cidr

93. Restore IP Addresses

Problem:

Given a string containing only digits, restore it by returning all possible valid IP address combinations.

Example:

Input: "25525511135"
Output: ["255.255.11.135", "255.255.111.35"]

Solution:

Backtracking. Note that leading '0' is not allowed except just '0'.

/**
 * @param {string} s
 * @return {string[]}
 */
let restoreIpAddresses = function(s, i = 0, path = [], result = []) {
  if (i === s.length) {
    if (path.length === 4) {
      result.push(path.join('.'))
    }
    return result
  }

  const digit = s.charCodeAt(i) - 48

  if (i === 0) {
    path[0] = digit
    restoreIpAddresses(s, i + 1, path, result)
    path[0] = 0
    return result
  }

  const sum = path[path.length - 1] * 10 + digit

  if (digit < sum && sum <= 255) {
    path[path.length - 1] = sum
    restoreIpAddresses(s, i + 1, path, result)
    path[path.length - 1] = (sum - digit) / 10
  }

  if (path.length < 4) {
    path.push(digit)
    restoreIpAddresses(s, i + 1, path, result)
    path.pop()
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “String”: https://leetcode.com/tag/string “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming

97. Interleaving String

Problem:

Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.

Example 1:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false

Solution:

Define f(i, j) to be whether s3[0...i+j-1) can be formed by the interleaving of s1[0...i) and s2[0...j).

f(i, j) = true, i <= 0 || j <= 0 // meaningless, skipped
f(i, j) = f(i-1, j) && s1[i-1] == s3[i+j-1] || f(i, j-1) && s2[j-1] == s3[i+j-1], 0 < i <= len(s1), 0 < j <= len(s2)

Dynamic array can be used.

/**
 * @param {string} s1
 * @param {string} s2
 * @param {string} s3
 * @return {boolean}
 */
let isInterleave = function(s1, s2, s3) {
  const len1 = s1.length
  const len2 = s2.length
  const len3 = s3.length
  if (len1 + len2 !== len3) { return false }
  if (len1 <= 0) { return s2 === s3 }
  if (len2 <= 0) { return s1 === s3 }

  const dp = []
  for (let i = 0; i <= len1; i++) {
    for (let j = 0; j <= len2; j++) {
      dp[j] = (i <= 0 || dp[j]) && s1[i-1] === s3[i+j-1] ||
              (j <= 0 || dp[j-1]) && s2[j-1] === s3[i+j-1]
    }
  }
  return dp[len2]
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search

100. Same Tree

Problem:

Given two binary trees, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical and the nodes have the same value.

Example 1:

Input:     1         1
          / \       / \
         2   3     2   3

        [1,2,3],   [1,2,3]

Output: true

Example 2:

Input:     1         1
          /           \
         2             2

        [1,2],     [1,null,2]

Output: false

Example 3:

Input:     1         1
          / \       / \
         2   1     1   2

        [1,2,1],   [1,1,2]

Output: false

Solution:

The code should be self-evident.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
let isSameTree = function(p, q) {
  return p === null && q === null ||
    p !== null && q !== null && p.val === q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right)
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search

101. Symmetric Tree

Problem:

Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

1
   / \
  2   2
 / \ / \
3  4 4  3

But the following [1,2,2,null,3,null,3] is not:

1
   / \
  2   2
   \   \
   3    3

Note:
Bonus points if you could solve it both recursively and iteratively.

Solution:

ONE

The result of pre-order and post-order traversal on a symmetric tree should be the same.

So just like 100. Same Tree. Except one is pre-order traversal and the other is post-order.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
let isSymmetric = function(root) {
  return root === null || isSymmetricTree(root.left, root.right)
};

/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
function isSymmetricTree (p, q) {
  return p === null && q === null ||
    p !== null && q !== null && p.val === q.val && isSymmetricTree(p.left, q.right) && isSymmetricTree(p.right, q.left)
};

TWO

Level order traversal. Check symmetry before entering the next level.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
let isSymmetric = function(root) {
  if (root === null) { return true }

  const queue = [NaN, root]

  while (queue.length > 1) {
    const node = queue.shift()
    if (node !== node) {
      for (let i = 0, j = queue.length-1; i <= j; i++, j--) {
        if (queue[i] === null && queue[j] !== null ||
            queue[i] !== null && queue[j] === null ||
            queue[i] !== null && queue[j] !== null && queue[i].val !== queue[j].val
           ) {
          return false
        }
      }
      queue.push(NaN)
    } else {
      if (node !== null) {
        queue.push(node.left)
        queue.push(node.right)
      }
    }
  }

  return true
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Tree”: https://leetcode.com/tag/tree “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search Similar Questions: “Binary Tree Zigzag Level Order Traversal”: https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal “Binary Tree Level Order Traversal II”: https://leetcode.com/problems/binary-tree-level-order-traversal-ii “Minimum Depth of Binary Tree”: https://leetcode.com/problems/minimum-depth-of-binary-tree “Binary Tree Vertical Order Traversal”: https://leetcode.com/problems/binary-tree-vertical-order-traversal “Average of Levels in Binary Tree”: https://leetcode.com/problems/average-of-levels-in-binary-tree “N-ary Tree Level Order Traversal”: https://leetcode.com/problems/n-ary-tree-level-order-traversal

102. Binary Tree Level Order Traversal

Problem:

Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

For example:
Given binary tree [3,9,20,null,null,15,7],

3
   / \
  9  20
    /  \
   15   7

return its level order traversal as:

[
  [3],
  [9,20],
  [15,7]
]

Solution:

The code should be self-evident.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
let levelOrder = function(root) {
  if (!root) { return [] }

  const result = []
  const queue = [NaN, root]
  while (queue.length > 1) {
    const node = queue.shift()
    if (node !== node) {
      result.push(queue.map(n => n.val))
      queue.push(NaN)
    } else {
      if (node.left) { queue.push(node.left) }
      if (node.right) { queue.push(node.right) }
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Stack”: https://leetcode.com/tag/stack “Tree”: https://leetcode.com/tag/tree “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search Similar Questions: “Binary Tree Level Order Traversal”: https://leetcode.com/problems/binary-tree-level-order-traversal

103. Binary Tree Zigzag Level Order Traversal

Problem:

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

3
   / \
  9  20
    /  \
   15   7

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

Solution:

Reverse the level when pushing to the reuslt.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
let zigzagLevelOrder = function(root) {
  if (!root) { return [] }

  const result = []
  const queue = [NaN, root]
  let zipzag = false
  while (queue.length > 1) {
    const node = queue.shift()
    if (node !== node) {
      if (zipzag = !zipzag) {
        result.push(queue.map(n => n.val))
      } else {
        result.push(queue.map(n => n.val).reverse())
      }
      queue.push(NaN)
    } else {
      if (node.left) { queue.push(node.left) }
      if (node.right) { queue.push(node.right) }
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Balanced Binary Tree”: https://leetcode.com/problems/balanced-binary-tree “Minimum Depth of Binary Tree”: https://leetcode.com/problems/minimum-depth-of-binary-tree “Maximum Depth of N-ary Tree”: https://leetcode.com/problems/maximum-depth-of-n-ary-tree

104. Maximum Depth of Binary Tree

Problem:

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its depth = 3.

Solution:

The code should be self-evident.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let maxDepth = function(root) {
  return root === null
    ? 0
    : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Construct Binary Tree from Inorder and Postorder Traversal”: https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal

105. Construct Binary Tree from Preorder and Inorder Traversal

Problem:

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]

Return the following binary tree:

    3
   / \
  9  20
    /  \
   15   7

Solution:

Pattern of preorder traversal result: pre(root) = root + pre(root.left) + pre(root.right)

Pattern of inorder traversal result: in(root) = in(root.left) + root + in(root.right)

There are no duplicates so get the first item in preorder result, pinpoint it in inorder result. Then we know the size of left and right subtree.

Repeat the process on subtrees.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
let buildTree = function(preorder, inorder) {
  return _buildTree(preorder, inorder, 0, preorder.length, 0, inorder.length)
};

function _buildTree (preorder, inorder, pStart, pEnd, iStart, iEnd) {
  if (pStart >= pEnd || iStart >= iEnd) {
    return null
  }
  const val = preorder[pStart]
  const node = new TreeNode(val)
  for (let i = iStart; i < iEnd; i++) {
    if (val === inorder[i]) {
      node.left = _buildTree(preorder, inorder, pStart + 1, i - iStart + (pStart + 1), iStart, i)
      node.right = _buildTree(preorder, inorder, (i + 1) - iEnd + pEnd, pEnd, i + 1, iEnd)
      break
    }
  }
  return node
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Construct Binary Tree from Preorder and Inorder Traversal”: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal

106. Construct Binary Tree from Inorder and Postorder Traversal

Problem:

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]

Return the following binary tree:

    3
   / \
  9  20
    /  \
   15   7

Solution:

Pattern of inorder traversal result: in(root) = in(root.left) + root + in(root.right)

Pattern of postorder traversal result: post(root) = post(root.left) + post(root.right) + root

There are no duplicates so get the first item in preorder result, pinpoint it in inorder result. Then we know the size of left and right subtree.

Repeat the process on subtrees.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
let buildTree = function(inorder, postorder) {
  return _buildTree(postorder, inorder, 0, postorder.length, 0, inorder.length)
};

function _buildTree (postorder, inorder, pStart, pEnd, iStart, iEnd) {
  if (pStart >= pEnd || iStart >= iEnd) {
    return null
  }
  const val = postorder[pEnd - 1]
  const node = new TreeNode(val)
  for (let i = iStart; i < iEnd; i++) {
    if (val === inorder[i]) {
      node.left = _buildTree(postorder, inorder, pStart, i - iStart + pStart, iStart, i)
      node.right = _buildTree(postorder, inorder, (i + 1) - iEnd + (pEnd - 1), pEnd - 1, i + 1, iEnd)
      break
    }
  }
  return node
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search Similar Questions: “Binary Tree Level Order Traversal”: https://leetcode.com/problems/binary-tree-level-order-traversal “Average of Levels in Binary Tree”: https://leetcode.com/problems/average-of-levels-in-binary-tree

107. Binary Tree Level Order Traversal II

Problem:

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example:
Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its bottom-up level order traversal as:

[
  [15,7],
  [9,20],
  [3]
]

Solution:

See 102. Binary Tree Level Order Traversal.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
let levelOrderBottom = function(root) {
  if (!root) { return [] }

  const result = []
  const queue = [NaN, root]
  while (queue.length > 1) {
    const node = queue.shift()
    if (node !== node) {
      result.unshift(queue.map(n => n.val))
      queue.push(NaN)
    } else {
      if (node.left) { queue.push(node.left) }
      if (node.right) { queue.push(node.right) }
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Maximum Depth of Binary Tree”: https://leetcode.com/problems/maximum-depth-of-binary-tree

110. Balanced Binary Tree

Problem:

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

Given the following tree [3,9,20,null,null,15,7]:

    3
   / \
  9  20
    /  \
   15   7

Return true.

Example 2:

Given the following tree [1,2,2,3,3,null,null,4,4]:

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4

Return false.

Solution:

Get the depth of subtrees and compare. Prune the DFS tree by returning -1.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
let isBalanced = function(root) {
  return getDepth(root) >= 0
};

function getDepth (root) {
  if (!root) { return 0 }
  const leftDepth = getDepth(root.left)
  if (leftDepth < 0) { return -1 }
  const rightDepth = getDepth(root.right)
  if (rightDepth < 0) { return -1 }
  return Math.abs(leftDepth - rightDepth) <= 1 ? Math.max(leftDepth, rightDepth) + 1 : -1
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search Similar Questions: “Binary Tree Level Order Traversal”: https://leetcode.com/problems/binary-tree-level-order-traversal “Maximum Depth of Binary Tree”: https://leetcode.com/problems/maximum-depth-of-binary-tree

111. Minimum Depth of Binary Tree

Problem:

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its minimum depth = 2.

Solution:

Ignore null children.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let minDepth = function(root) {
  if (!root) { return 0 }
  if (root.left !== null && root.right !== null) {
    return Math.min(minDepth(root.left), minDepth(root.right)) + 1
  } else if (root.left !== null) {
    return minDepth(root.left) + 1
  } else {
    return minDepth(root.right) + 1
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Path Sum II”: https://leetcode.com/problems/path-sum-ii “Binary Tree Maximum Path Sum”: https://leetcode.com/problems/binary-tree-maximum-path-sum “Sum Root to Leaf Numbers”: https://leetcode.com/problems/sum-root-to-leaf-numbers “Path Sum III”: https://leetcode.com/problems/path-sum-iii “Path Sum IV”: https://leetcode.com/problems/path-sum-iv

112. Path Sum

Problem:

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

Solution:

Note that node value could be negative so pruning can not be performed.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {boolean}
 */
let hasPathSum = function(root, sum) {
  if (!root) { return false }
  if (root.left === null && root.right === null) { return root.val === sum }
  return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val)
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Path Sum”: https://leetcode.com/problems/path-sum “Binary Tree Paths”: https://leetcode.com/problems/binary-tree-paths “Path Sum III”: https://leetcode.com/problems/path-sum-iii “Path Sum IV”: https://leetcode.com/problems/path-sum-iv

113. Path Sum II

Problem:

Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

Return:

[
   [5,4,11,2],
   [5,8,4,5]
]

Solution:

Simple backtracking.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {number[][]}
 */
let pathSum = function(root, sum, path = [], result = []) {
  if (!root) { return result }

  if (root.left === null && root.right === null) {
    if (root.val === sum) {
      result.push([...path, root.val])
    }
    return result
  }

  path.push(root.val)
  pathSum(root.left, sum - root.val, path, result)
  pathSum(root.right, sum - root.val, path, result)
  path.pop()

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Flatten a Multilevel Doubly Linked List”: https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list

114. Flatten Binary Tree to Linked List

Problem:

Given a binary tree, flatten it to a linked list in-place.

For example, given the following tree:

    1
   / \
  2   5
 / \   \
3   4   6

The flattened tree should look like:

1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

Solution:

Return the leaf node of a flattened subtree for concatenation.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
let flatten = function(root) {
  _flatten(root)
};

/**
 * @param {TreeNode} root
 * @return {TreeNode} leaf node of a flattened subtree
 */
function _flatten (root) {
  if (!root) { return null }
  const leftLeaf = _flatten(root.left)
  const rightLeaf = _flatten(root.right)
  if (leftLeaf !== null) {
    leftLeaf.right = root.right
    root.right = root.left
  } else if (rightLeaf === null) {
    return root
  }

  root.left = null
  return rightLeaf || leftLeaf
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “String”: https://leetcode.com/tag/string “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming

115. Distinct Subsequences

Problem:

Given a string S and a string T, count the number of distinct subsequences of S which equals T.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).

Example 1:

Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:

As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

Example 2:

Input: S = "babgbag", T = "bag"
Output: 5
Explanation:

As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)

babgbag
^^ ^
babgbag
^^    ^
babgbag
^    ^^
babgbag
  ^  ^^
babgbag
    ^^^

Solution:

Define f(i, j) to be the number of ways that generate T[0...j) from S[0...i).

For f(i, j) you can always skip S[i-1], but can only take it when S[i-1] === T[j-1].

f(0, j) = 0, j > 0 // nothing to delete
f(i, 0) = 1 // delete all
f(i, j) = f(i-1, j) + (S[i-1] === T[j-1] ? f(i-1, j-1) : 0)

Dynamic array can be used.

/**
 * @param {string} s
 * @param {string} t
 * @return {number}
 */
let numDistinct = function(s, t) {
  const lens = s.length
  const lent = t.length
  const dp = new Array(lent + 1).fill(0)
  dp[0] = 1
  for (let i = 1; i <= lens; i++) {
    for (let j = lent; j >= 1; j--) {
      if (s[i-1] === t[j-1]) {
        dp[j] += dp[j-1]
      }
    }
  }
  return dp[lent]
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Populating Next Right Pointers in Each Node II”: https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii “Binary Tree Right Side View”: https://leetcode.com/problems/binary-tree-right-side-view

116. Populating Next Right Pointers in Each Node

Problem:

Given a binary tree

struct TreeLinkNode {
  TreeLinkNode *left;
  TreeLinkNode *right;
  TreeLinkNode *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Note:

• You may only use constant extra space.
• Recursive approach is fine, implicit stack space does not count as extra space for this problem.
• You may assume that it is a perfect binary tree (ie, all leaves are at the same level, and every parent has two children).

Example:

Given the following perfect binary tree,

     1
   /  \
  2    3
 / \  / \
4  5  6  7

After calling your function, the tree should look like:

     1 -> NULL
   /  \
  2 -> 3 -> NULL
 / \  / \
4->5->6->7 -> NULL

Solution:

ONE

Recursive.

For every node:

• Left child: points to node.right.
• Right child: points to node.next.left if node.next exists.

/**
 * Definition for binary tree with next pointer.
 * function TreeLinkNode(val) {
 *     this.val = val;
 *     this.left = this.right = this.next = null;
 * }
 */

/**
 * @param {TreeLinkNode} root
 * @return {void} Do not return anything, modify tree in-place instead.
 */
let connect = function(root) {
  if (!root) { return }
  if (root.left !== null) {
    root.left.next = root.right
    connect(root.left)
  }
  if (root.right !== null) {
    if (root.next !== null) {
      root.right.next = root.next.left
    }
    connect(root.right)
  }
};

TWO

Level order traversal.

/**
 * Definition for binary tree with next pointer.
 * function TreeLinkNode(val) {
 *     this.val = val;
 *     this.left = this.right = this.next = null;
 * }
 */

/**
 * @param {TreeLinkNode} root
 * @return {void} Do not return anything, modify tree in-place instead.
 */
let connect = function(root) {
  if (!root) { return }

  const queue = [NaN, root]
  while (queue.length > 1) {
    const node = queue.shift()
    if (node !== node) {
      for (let i = 0; i < queue.length; i++) {
        queue[i].next = queue[i+1] || null
      }
      queue.push(NaN)
    } else {
      if (node.left !== null) { queue.push(node.left) }
      if (node.right !== null) { queue.push(node.right) }
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Populating Next Right Pointers in Each Node”: https://leetcode.com/problems/populating-next-right-pointers-in-each-node

117. Populating Next Right Pointers in Each Node II

Problem:

Given a binary tree

struct TreeLinkNode {
  TreeLinkNode *left;
  TreeLinkNode *right;
  TreeLinkNode *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Note:

• You may only use constant extra space.
• Recursive approach is fine, implicit stack space does not count as extra space for this problem.

Example:

Given the following binary tree,

     1
   /  \
  2    3
 / \    \
4   5    7

After calling your function, the tree should look like:

     1 -> NULL
   /  \
  2 -> 3 -> NULL
 / \    \
4-> 5 -> 7 -> NULL

Solution:

ONE

Recursive. See 116. Populating Next Right Pointers in Each Node.

The tree may not be perfect now. So keep finding next until there is a node with children, or null.

This also means post-order traversal is required.

/**
 * Definition for binary tree with next pointer.
 * function TreeLinkNode(val) {
 *     this.val = val;
 *     this.left = this.right = this.next = null;
 * }
 */

/**
 * @param {TreeLinkNode} root
 * @return {void} Do not return anything, modify tree in-place instead.
 */
let connect = function(root) {
  if (!root) { return }
  let next = null
  for (let node = root.next; node !== null; node = node.next) {
    if (node.left !== null) {
      next = node.left
      break
    }
    if (node.right !== null) {
      next = node.right
      break
    }
  }
  if (root.right !== null) {
    root.right.next = next
  }
  if (root.left !== null) {
    root.left.next = root.right || next
  }
  connect(root.right)
  connect(root.left)
};

TWO

Level order traversal. Exact same as 116. Populating Next Right Pointers in Each Node.

/**
 * Definition for binary tree with next pointer.
 * function TreeLinkNode(val) {
 *     this.val = val;
 *     this.left = this.right = this.next = null;
 * }
 */

/**
 * @param {TreeLinkNode} root
 * @return {void} Do not return anything, modify tree in-place instead.
 */
let connect = function(root) {
  if (!root) { return }

  const queue = [NaN, root]
  while (queue.length > 1) {
    const node = queue.shift()
    if (node !== node) {
      for (let i = 0; i < queue.length; i++) {
        queue[i].next = queue[i+1] || null
      }
      queue.push(NaN)
    } else {
      if (node.left !== null) { queue.push(node.left) }
      if (node.right !== null) { queue.push(node.right) }
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Pascal’s Triangle II”: https://leetcode.com/problems/pascals-triangle-ii

118. Pascal’s Triangle

Problem:

Given a non-negative integer numRows, generate the first numRows of Pascal’s triangle.

In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 5
Output:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

Solution:

Dynamic Programming 101.

/**
 * @param {number} numRows
 * @return {number[][]}
 */
let generate = function(numRows) {
  if (numRows <= 0) { return [] }

  const result = [[1]]
  for (let i = 1; i < numRows; i++) {
    const lastRow = result[i-1]
    const row = [1]
    for (let j = 1; j < i; j++) {
      row[j] = lastRow[j] + lastRow[j-1]
    }
    row.push(1)
    result.push(row)
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array Similar Questions: “Pascal’s Triangle”: https://leetcode.com/problems/pascals-triangle

119. Pascal’s Triangle II

Problem:

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.

Note that the row index starts from 0.

In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O(k) extra space?

Solution:

Dynamic Programming 101 with dynamic array.

State (i, j) depends on (i-1, j) and (i-1, j-1). So to access (i-1, j-1) iteration must be from right to left.

/**
 * @param {number} rowIndex
 * @return {number[]}
 */
let getRow = function(rowIndex) {
  if (rowIndex < 0) { return [] }

  const row = [1]
  for (let i = 1; i <= rowIndex; i++) {
    for (let j = i - 1; j > 0; j--) {
      row[j] += row[j-1]
    }
    row.push(1)
  }

  return row
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Array”: https://leetcode.com/tag/array “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming

120. Triangle

Problem:

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:

Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

Solution:

Define f(i, j) to be the minimum path sum from triangle[0][0] to triangle[i][j].

f(i, 0) = f(i-1, j) + triangle[i][0]
f(i, j) = min( f(i-1, j-1), f(i-1, j) ) + triangle[i][j], 0 < j < i
f(i, i) = f(i-1, i-1) + triangle[i][i], i > 0

Dynamic array can be used.

/**
 * @param {number[][]} triangle
 * @return {number}
 */
let minimumTotal = function(triangle) {
  if (triangle.length <= 0) { return 0 }

  const dp = [triangle[0][0]]
  for (let i = 1; i < triangle.length; i++) {
    dp[i] = dp[i-1] + triangle[i][i]
    for (let j = i - 1; j >= 1; j--) {
      dp[j] = Math.min(dp[j], dp[j-1]) + triangle[i][j]
    }
    dp[0] += triangle[i][0]
  }
  return Math.min(...dp)
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “Maximum Subarray”: https://leetcode.com/problems/maximum-subarray “Best Time to Buy and Sell Stock II”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii “Best Time to Buy and Sell Stock III”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii “Best Time to Buy and Sell Stock IV”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv “Best Time to Buy and Sell Stock with Cooldown”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown

121. Best Time to Buy and Sell Stock

Problem:

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Solution:

Only care about positive profits. Take the frist item as base and scan to the right. If we encounter an item j whose price price[j] is lower than the base (which means if we sell now the profit would be negative), we sell j-1 instead and make j the new base.

Because price[j] is lower that the base, using j as new base is guaranteed to gain more profit comparing to the old one.

/**
 * @param {number[]} prices
 * @return {number}
 */
let maxProfit = function(prices) {
  let max = 0
  let base = prices[0]
  for (let i = 1; i < prices.length; i++) {
    const profit = prices[i] - base
    if (profit > max) {
      max = profit
    } else if (profit < 0) {
      base = prices[i]
    }
  }
  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Array”: https://leetcode.com/tag/array “Greedy”: https://leetcode.com/tag/greedy Similar Questions: “Best Time to Buy and Sell Stock”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock “Best Time to Buy and Sell Stock III”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii “Best Time to Buy and Sell Stock IV”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv “Best Time to Buy and Sell Stock with Cooldown”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown “Best Time to Buy and Sell Stock with Transaction Fee”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee

122. Best Time to Buy and Sell Stock II

Problem:

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
             Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Solution:

Sell immediately after the price drops. Or in other perspective, it is the sum of all the incremental pairs (buy in then immediately sell out).

/**
 * @param {number[]} prices
 * @return {number}
 */
let maxProfit = function(prices) {
  let max = 0
  for (let i = 1; i < prices.length; i++) {
    if (prices[i] > prices[i-1]) {
      max += prices[i] - prices[i-1]
    }
  }
  return max
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Dynamic Programming”: https://leetcode.com/tag/dynamic-programming Similar Questions: “Best Time to Buy and Sell Stock”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock “Best Time to Buy and Sell Stock II”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii “Best Time to Buy and Sell Stock IV”: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv “Maximum Sum of 3 Non-Overlapping Subarrays”: https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays

123. Best Time to Buy and Sell Stock III

Problem:

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

**Note:**You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
             Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Solution:

Multiple transactions may not be engaged in at the same time. That means if we view the days that involed in the same transaction as a group, there won’t be any intersection. We may complete at most two transactions, so divide the days into two groups, [0...k] and [k...n-1]. Notice k exists in both groups because technically we can sell out then immediately buy in at the same day.

Define p1(i) to be the max profit of day [0...i]. This is just like the problem of 121. Best Time to Buy and Sell Stock.

p1(0) = 0
p1(i) = max( p1(i-1), prices[i] - min(prices[0], ..., prices[i-1]) ), 0 < i <= n-1

Define p2(i) to be the max profit of day [i...n-1]. This is the mirror of p1.

p2(n-1) = 0
p2(i) = max( p2(i+1), max(prices[i], ..., prices[n-1]) - prices[i] ), n-1 > i >= 0

Define f(k) to be p1(k) + p2(k). We need to get max( f(0), ..., f(n-1) ).

/**
 * @param {number[]} prices
 * @return {number}
 */
let maxProfit = function(prices) {
  const len = prices.length
  if (len <= 1) { return 0 }

  const dp = [0]

  let min = prices[0]
  for (let i = 1; i < len; i++) {
    dp[i] = Math.max(dp[i-1], prices[i] - min)
    min = Math.min(prices[i], min)
  }

  let p2 = 0
  let max = prices[len-1]
  for (let i = len-2; i >= 0; i--) {
    max = Math.max(prices[i], max)
    p2 = Math.max(p2, max - prices[i])
    dp[i] += p2
  }

  return Math.max(...dp)
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Path Sum”: https://leetcode.com/problems/path-sum “Sum Root to Leaf Numbers”: https://leetcode.com/problems/sum-root-to-leaf-numbers “Path Sum IV”: https://leetcode.com/problems/path-sum-iv “Longest Univalue Path”: https://leetcode.com/problems/longest-univalue-path

124. Binary Tree Maximum Path Sum

Problem:

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42

Solution:

For every node, there are six possible ways to get the max path sum:

• With node.val
  1. node.val plus the max sum of a path that ends with node.left.
  2. node.val plus the max sum of a path that starts with node.right.
  3. node.val plus the max sum of both paths.
  4. Just node.val (the max sum of both paths are negative).
• Withoutnode.val (disconnected)
  1. The max-sum path is somewhere under the node.left subtree.
  2. The max-sum path is somewhere under the node.right subtree.

There are two ways to implement this.

ONE

Define a function that returns two values. The max sum of a path that may or may not end with root node, and the max sum of the path that ends with root node.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let maxPathSum = function(root) {
  return Math.max(..._maxPathSum(root))
};

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
function _maxPathSum (root) {
  if (!root) { return [-Infinity, -Infinity] }

  const left = _maxPathSum(root.left)
  const right = _maxPathSum(root.right)
  return [
    Math.max(left[0], right[0], root.val + Math.max(0, left[1], right[1], left[1] + right[1])),
    Math.max(left[1], right[1], 0) + root.val
  ]
}

TWO

Just return the later (max sum of a path that ends with root). Maintain a global variable to store the disconnected max sum.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let maxPathSum = function(root) {
  const global = { max: -Infinity }
  _maxPathSum(root, global)
  return global.max
};


/**
 * @param {TreeNode} root
 * @param {object} global
 * @param {number} global.max
 * @return {number[]}
 */
function _maxPathSum (root, global) {
  if (!root) { return -Infinity }

  const left = _maxPathSum(root.left, global)
  const right = _maxPathSum(root.right, global)
  const localMax = Math.max(left, right, 0) + root.val
  global.max = Math.max(global.max, localMax, root.val + left + right)
  return localMax
}

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Easy Related Topics: “Two Pointers”: https://leetcode.com/tag/two-pointers “String”: https://leetcode.com/tag/string Similar Questions: “Palindrome Linked List”: https://leetcode.com/problems/palindrome-linked-list “Valid Palindrome II”: https://leetcode.com/problems/valid-palindrome-ii

125. Valid Palindrome

Problem:

Given a string, determine if it is a palindrome, considering only alphanumeric characters and ignoring cases.

Note: For the purpose of this problem, we define empty string as valid palindrome.

Example 1:

Input: "A man, a plan, a canal: Panama"
Output: true

Example 2:

Input: "race a car"
Output: false

Solution:

ONE

/**
 * @param {string} s
 * @return {boolean}
 */
let isPalindrome = function(s) {
  const clean = s.toLowerCase().split(/[^a-z0-9]*/)
  return clean.join('') === clean.reverse().join('')
};

TWO

Remove non-alphanumeric characters then compare.

/**
 * @param {string} s
 * @return {boolean}
 */
let isPalindrome = function(s) {
  const clean = s.replace(/[^a-zA-Z0-9]/g, '').toLowerCase()
  for (let i = 0, j = clean.length - 1; i < j; i++, j--) {
    if (clean[i] !== clean[j]) { return false }
  }
  return true
};

THREE

Compare the char codes.

/**
 * @param {string} s
 * @return {boolean}
 */
let isPalindrome = function(s) {
  for (let i = 0, j = s.length - 1; i < j; i++, j--) {
    let left = s.charCodeAt(i)
    while (i < j && (left < 48 || left > 57 && left < 65 || left > 90 && left < 97 || left > 122)) {
      left = s.charCodeAt(++i)
    }
    if (i >= j) { return true }
    if (left >= 65 && left <= 90) {
      left += 32
    }

    let right = s.charCodeAt(j)
    while (i < j && (right < 48 || right > 57 && right < 65 || right > 90 && right < 97 || right > 122)) {
      right = s.charCodeAt(--j)
    }
    if (i >= j) { return true }
    if (right >= 65 && right <= 90) {
      right += 32
    }

    if (left !== right) { return false }
  }

  return true
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “String”: https://leetcode.com/tag/string “Backtracking”: https://leetcode.com/tag/backtracking “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search Similar Questions: “Word Ladder”: https://leetcode.com/problems/word-ladder

126. Word Ladder II

Problem:

Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:

1. Only one letter can be changed at a time
2. Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

Note:

• Return an empty list if there is no such transformation sequence.
• All words have the same length.
• All words contain only lowercase alphabetic characters.
• You may assume no duplicates in the word list.
• You may assume beginWord and endWord are non-empty and are not the same.

Example 1:

Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output:
[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]

Example 2:

Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Output: []

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

Solution:

This is just like 127. Word Ladder.

The constrain still works, but instead of deleting the words right away, collect them and delete them all when a level ends, so that we can reuse the words (matching different parents in the same level).

The items in the queue are not just words now. Parent nodes are also kept so that we can backtrack the path from the end.

/**
 * @param {string} beginWord
 * @param {string} endWord
 * @param {string[]} wordList
 * @return {string[][]}
 */
function findLadders (beginWord, endWord, wordList) {
  wordList = new Set(wordList)
  if (!wordList.has(endWord)) { return [] }

  const ALPHABET = 'abcdefghijklmnopqrstuvwxyz'

  const result = []
  let isEndWordFound = false
  const levelWords = new Set()
  const queue = [[beginWord, null], null]
  while (queue.length > 1) {
    const node = queue.shift()

    if (node === null) {
      if (isEndWordFound) {
        break
      }
      levelWords.forEach(word => wordList.delete(word))
      levelWords.clear()
      queue.push(null)
      continue
    }

    const word = node[0]

    for (let i = word.length - 1; i >= 0; i--) {
      const head = word.slice(0, i)
      const tail = word.slice(i+1)

      for (let c = 0; c < 26; c++) {
        if (ALPHABET[c] !== word[i]) {
          const w = head + ALPHABET[c] + tail
          if (w === endWord) {
            const path = [endWord]
            for (let n = node; n !== null; n = n[1]) {
              path.unshift(n[0])
            }
            result.push(path)
            isEndWordFound = true
          }
          if (wordList.has(w)) {
            levelWords.add(w)
            queue.push([w, node])
          }
        }
      }
    }
  }

  return result
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search Similar Questions: “Word Ladder II”: https://leetcode.com/problems/word-ladder-ii “Minimum Genetic Mutation”: https://leetcode.com/problems/minimum-genetic-mutation

127. Word Ladder

Problem:

Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

1. Only one letter can be changed at a time.
2. Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

Note:

• Return 0 if there is no such transformation sequence.
• All words have the same length.
• All words contain only lowercase alphabetic characters.
• You may assume no duplicates in the word list.
• You may assume beginWord and endWord are non-empty and are not the same.

Example 1:

Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output: 5

Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.

Example 2:

Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Output: 0

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

Solution:

Think of it as building a tree, with begineWord as root and endWord as leaves.

The best way control the depth (length of the shortest transformations) while building the tree is level-order traversal (BFS).

We do not actually build the tree because it is expensive (astronomical if the list is huge). In fact, we only need one shortest path. So just like Dijkstra’s algorithm, we say that the first time (level i) we encounter a word that turns out to be in a shortest path, then level i is the lowest level this word could ever get. We can safely remove it from the wordList.

To find all the next words, instead of filtering the wordList, enumerate all 25 possible words and check if in wordList.

/**
 * @param {string} beginWord
 * @param {string} endWord
 * @param {string[]} wordList
 * @return {number}
 */
let ladderLength = function(beginWord, endWord, wordList) {
  wordList = new Set(wordList)
  if (!wordList.has(endWord)) { return 0 }

  const ALPHABET = 'abcdefghijklmnopqrstuvwxyz'

  let level = 1
  const queue = [beginWord, null]
  while (queue.length > 1) {
    const word = queue.shift()

    if (word === null) {
      level++
      queue.push(null)
      continue
    }

    for (let i = word.length - 1; i >= 0; i--) {
      const head = word.slice(0, i)
      const tail = word.slice(i+1)

      for (let c = 0; c < 26; c++) {
        if (ALPHABET[c] !== word[i]) {
          const word = head + ALPHABET[c] + tail
          if (word === endWord) {
            return level + 1
          }
          if (wordList.delete(word)) {
            queue.push(word)
          }
        }
      }
    }
  }

  return 0
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Hard Related Topics: “Array”: https://leetcode.com/tag/array “Union Find”: https://leetcode.com/tag/union-find Similar Questions: “Binary Tree Longest Consecutive Sequence”: https://leetcode.com/problems/binary-tree-longest-consecutive-sequence

128. Longest Consecutive Sequence

Problem:

Given an unsorted array of integers, find the length of the longest consecutive elements sequence.

Your algorithm should run in O(n) complexity.

Example:

Input: [100, 4, 200, 1, 3, 2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.

Solution:

Build a Set from the list. Pick a number, find all it’s adjacent numbers that are also in the Set. Count them and remove them all from the Set. Repeat until the Set is empty. Time complexity O(n + n) = O(n).

/**
 * @param {number[]} nums
 * @return {number}
 */
let longestConsecutive = function(nums) {
  const numSet = new Set(nums)
  let maxCount = 0
  while (numSet.size > 0) {
    const num = numSet.values().next().value
    numSet.delete(num)
    let count = 1
    for (let n = num + 1; numSet.delete(n); n++) {
      count++
    }
    for (let n = num - 1; numSet.delete(n); n--) {
      count++
    }
    if (count > maxCount) {
      maxCount = count
    }
  }
  return maxCount
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Tree”: https://leetcode.com/tag/tree “Depth-first Search”: https://leetcode.com/tag/depth-first-search Similar Questions: “Path Sum”: https://leetcode.com/problems/path-sum “Binary Tree Maximum Path Sum”: https://leetcode.com/problems/binary-tree-maximum-path-sum

129. Sum Root to Leaf Numbers

Problem:

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:

Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Solution:

To write a clean solution for this promblem, use 0 as indicator of leaf node. If all the children get 0, it is a leaf node, return the sum of current level.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
let sumNumbers = function(root, sum = 0) {
  if (!root) { return 0 }
  sum = sum * 10 + root.val
  return sumNumbers(root.left, sum) + sumNumbers(root.right, sum) || sum
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Depth-first Search”: https://leetcode.com/tag/depth-first-search “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search “Union Find”: https://leetcode.com/tag/union-find Similar Questions: “Number of Islands”: https://leetcode.com/problems/number-of-islands “Walls and Gates”: https://leetcode.com/problems/walls-and-gates

130. Surrounded Regions

Problem:

Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example:

X X X X
X O O X
X X O X
X O X X

After running your function, the board should be:

X X X X
X X X X
X X X X
X O X X

Explanation:

Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Solution:

Find all the Os that are connected to the Os on the border, change them to #. Then scan the board, change O to X and # back to O.

The process of finding the connected Os is just like tree traversal. Os on the border are the same level. Their children are the second level. And so on.

So both BFS and DFS are good. I prefer BFS when pruning is not needed in favor of its readability.

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
let solve = function(board) {
  const height = board.length
  if (height <= 1) { return }
  const width = board[0].length
  if (width <= 1) { return }

  const rowend = height - 1
  const colend = width - 1

  const queue = []

  for (let row = 0; row < height; row++) {
    if (board[row][0] === 'O') {
      board[row][0] = '#'
      queue.push(row, 0)
    }
    if (board[row][colend] === 'O') {
      board[row][colend] = '#'
      queue.push(row, colend)
    }
  }

  for (let col = 0; col < width; col++) {
    if (board[0][col] === 'O') {
      board[0][col] = '#'
      queue.push(0, col)
    }
    if (board[rowend][col] === 'O') {
      board[rowend][col] = '#'
      queue.push(rowend, col)
    }
  }

  while (queue.length > 0) {
    const row = queue.shift()
    const col = queue.shift()
    if (row < rowend && board[row + 1][col] === 'O') {
      board[row + 1][col] = '#'
      queue.push(row + 1, col)
    }
    if (row > 0 && board[row - 1][col] === 'O') {
      board[row - 1][col] = '#'
      queue.push(row - 1, col)
    }
    if (board[row][col + 1] === 'O') {
      board[row][col + 1] = '#'
      queue.push(row, col + 1)
    }
    if (board[row][col - 1] === 'O') {
      board[row][col - 1] = '#'
      queue.push(row, col - 1)
    }
  }

  for (let row = 0; row < height; row++) {
    for (let col = 0; col < width; col++) {
      if (board[row][col] === '#') {
        board[row][col] = 'O'
      } else if (board[row][col] === 'O') {
        board[row][col] = 'X'
      }
    }
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

Difficulty: Medium Related Topics: “Depth-first Search”: https://leetcode.com/tag/depth-first-search “Breadth-first Search”: https://leetcode.com/tag/breadth-first-search “Graph”: https://leetcode.com/tag/graph Similar Questions: “Copy List with Random Pointer”: https://leetcode.com/problems/copy-list-with-random-pointer

133. Clone Graph

Problem:

Given the head of a graph, return a deep copy (clone) of the graph. Each node in the graph contains a label (int) and a list (List[UndirectedGraphNode]) of its neighbors. There is an edge between the given node and each of the nodes in its neighbors.

OJ’s undirected graph serialization (so you can understand error output):

Nodes are labeled uniquely.

We use # as a separator for each node, and , as a separator for node label and each neighbor of the node.

As an example, consider the serialized graph {0,1,2#1,2#2,2}.

The graph has a total of three nodes, and therefore contains three parts as separated by #.

1. First node is labeled as 0. Connect node 0 to both nodes 1 and 2.
2. Second node is labeled as 1. Connect node 1 to node 2.
3. Third node is labeled as 2. Connect node 2 to node 2 (itself), thus forming a self-cycle.

Visually, the graph looks like the following:

       1
      / \
     /   \
    0 --- 2
         / \
         \_/

Note: The information about the tree serialization is only meant so that you can understand error output if you get a wrong answer. You don’t need to understand the serialization to solve the problem.

Solution:

DFS. Cache the visited node before entering the next recursion.

/**
 * Definition for undirected graph.
 * function UndirectedGraphNode(label) {
 *     this.label = label;
 *     this.neighbors = [];   // Array of UndirectedGraphNode
 * }
 */

/**
 * @param {UndirectedGraphNode} graph
 * @return {UndirectedGraphNode}
 */
let cloneGraph = function(graph) {
  const cache = {}
  return _clone(graph)

  function _clone (graph) {
    if (!graph) { return graph }
    const label = graph.label
    if (!cache[label]) {
      cache[label] = new UndirectedGraphNode(label)
      cache[label].neighbors = graph.neighbors.map(_clone)
    }
    return cache[label]
  }
};

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

☆: .｡. o(≧▽≦)o .｡.:☆☆: .｡. o(≧▽≦)o .｡.:☆

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
const upsideDownBinaryTree = function(root) {
  let curr = root
  let next = null
  let temp = null
  let prev = null
  while (curr !== null) {
    next = curr.left
    curr.left = temp
    temp = curr.right
    curr.right = prev
    prev = curr
    curr = next
  }
  return prev
}

// another

const upsideDownBinaryTree = function(root) {
  if (root == null || root.left == null) {
    return root
  }
  const newRoot = upsideDownBinaryTree(root.left)
  root.left.left = root.right
  root.left.right = root
  root.left = null
  root.right = null
  return newRoot
}

/**
 * @param {number[]} A
 * @return {number}
 */
const maxSubarraySumCircular = function(A) {
  let minSum = Infinity, sum = 0, maxSum = -Infinity, curMax = 0, curMin = 0
  for(let a of A) {
    sum += a
    curMax = Math.max(curMax + a, a);
    maxSum = Math.max(maxSum, curMax);
    curMin = Math.min(curMin + a, a);
    minSum = Math.min(minSum, curMin);
  }
  return  maxSum > 0 ? Math.max(maxSum, sum - minSum) : maxSum;
};

Balanced Binary Tree - LeetCode

Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

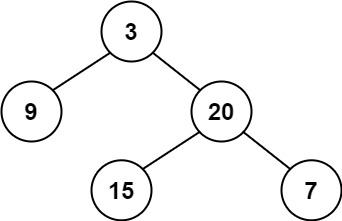
Input: root = $$3,9,20,null,null,15,7$$
Output: true

Example 2:

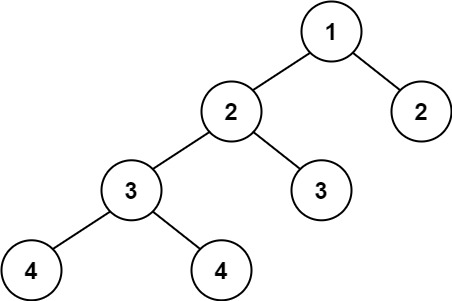
Input: root = $$1,2,2,3,3,null,null,4,4$$
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -104 <= Node.val <= 104

Source# Convert Sorted Array to Binary Search Tree

Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted array: $$-10,-3,0,5,9$$,

One possible answer is: $$0,-3,9,-10,null,5$$, which represents the following height balanced BST:

  0
 / \\

-3 9
/ /
-10 5

Source# Delete Node in a BST

Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.
2. If the node is found, delete the node.

Follow up: Can you solve it with time complexity O(height of tree)?

Example 1:

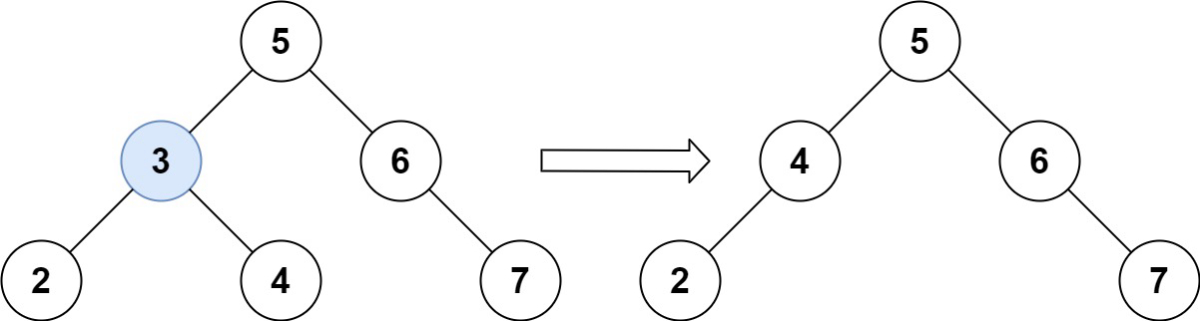
Input: root = $$5,3,6,2,4,null,7$$, key = 3
Output: $$5,4,6,2,null,null,7$$
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is $$5,4,6,2,null,null,7$$, shown in the above BST.
Please notice that another valid answer is $$5,2,6,null,4,null,7$$ and it’s also accepted.

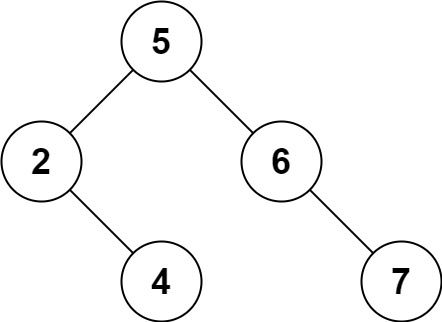
Example 2:

Input: root = $$5,3,6,2,4,null,7$$, key = 0
Output: $$5,3,6,2,4,null,7$$
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -105 <= Node.val <= 105
• Each node has a unique value.
• root is a valid binary search tree.
• -105 <= key <= 105

Source

/**
 * @param {number[][]} intervals
 * @return {number}
 */
const minMeetingRooms = function(intervals) {
  const len = intervals.length
  const starts = new Array(len)
  const ends = new Array(len)
  for (let i = 0; i < len; i++) {
    starts[i] = intervals[i][0]
    ends[i] = intervals[i][1]
  }
  starts.sort((a, b) => a - b)
  ends.sort((a, b) => a - b)
  let rooms = 0
  let endsIdx = 0
  for (let i = 0; i < len; i++) {
    if (starts[i] < ends[endsIdx]) rooms++
    else endsIdx++
  }
  return rooms
}

• 2. Add Two Numbers
  • Problem:
  • Solution:
• 4. Median of Two Sorted Arrays
  • Problem:
  • Solution:
• 6. ZigZag Conversion
  • Problem:
  • Solution:
• 7. Reverse Integer
  • Problem:
  • Solution:
    • ONE
    • TWO
• 8. String to Integer (atoi)
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 9. Palindrome Number
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 10. Regular Expression Matching
  • Problem:
  • Solution:
    • ONE
    • TWO
• 11. Container With Most Water
  • Problem:
  • Solution:
• 12. Integer to Roman
  • Problem:
  • Solution:
• 13. Roman to Integer
  • Problem:
  • Solution:
• 14. Longest Common Prefix
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 15. 3Sum
  • Problem:
  • Solution:
• 16. 3Sum Closest
  • Problem:
  • Solution:
• 17. Letter Combinations of a Phone Number
  • Problem:
  • Solution:
    • ONE
    • TWO
• 18. 4Sum
  • Problem:
  • Solution:
• 19. Remove Nth Node From End of List
  • Problem:
  • Solution:
• 20. Valid Parentheses
  • Problem:
  • Solution:
• 21. Merge Two Sorted Lists
  • Problem:
  • Solution:
• 22. Generate Parentheses
  • Problem:
  • Solution:
    • ONE
    • TWO
• 23. Merge k Sorted Lists
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 24. Swap Nodes in Pairs
  • Problem:
  • Solution:
• 25. Reverse Nodes in k-Group
  • Problem:
  • Solution:
• 26. Remove Duplicates from Sorted Array
  • Problem:
  • Solution:
• 27. Remove Element
  • Problem:
  • Solution:
• 29. Divide Two Integers
  • Problem:
  • Solution:
• 31. Next Permutation
  • Problem:
  • Solution:
• 33. Search in Rotated Sorted Array
  • Problem:
  • Solution:
• 34. Find First and Last Position of Element in Sorted Array
  • Problem:
  • Solution:
• 35. Search Insert Position
  • Problem:
  • Solution:
• 36. Valid Sudoku
  • Problem:
  • Solution:
• 37. Sudoku Solver
  • Problem:
  • Solution:
• 38. Count and Say
  • Problem:
  • Solution:
    • ONE
    • TWO
• 39. Combination Sum
  • Problem:
  • Solution:
• 40. Combination Sum II
  • Problem:
  • Solution:
• 41. First Missing Positive
  • Problem:
  • Solution:
• 42. Trapping Rain Water
  • Problem:
  • Solution:
• 43. Multiply Strings
  • Problem:
  • Solution:
• 45. Jump Game II
  • Problem:
  • Solution:
• 46. Permutations
  • Problem:
  • Solution:
• 47. Permutations II
  • Problem:
  • Solution:
• 48. Rotate Image
  • Problem:
  • Solution:
• 49. Group Anagrams
  • Problem:
  • Solution:
    • ONE
    • TWO
• 50. Pow(x, n)
  • Problem:
  • Solution:
• 51. N-Queens
  • Problem:
  • Solution:
    • ONE
    • TWO
• 52. N-Queens II
  • Problem:
  • Solution:
• 53. Maximum Subarray
  • Problem:
  • Solution:
• 54. Spiral Matrix
  • Problem:
  • Solution:
• 55. Jump Game
  • Problem:
  • Solution:
    • ONE
    • TWO
• 56. Merge Intervals
  • Problem:
  • Solution:
• 57. Insert Interval
  • Problem:
  • Solution:
• 58. Length of Last Word
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 59. Spiral Matrix II
  • Problem:
  • Solution:
• 60. Permutation Sequence
  • Problem:
  • Solution:
• 61. Rotate List
  • Problem:
  • Solution:
• 62. Unique Paths
  • Problem:
  • Solution:
• 64. Minimum Path Sum
  • Problem:
  • Solution:
• 65. Valid Number
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 66. Plus One
  • Problem:
  • Solution:
    • ONE
    • TWO
• 68. Text Justification
  • Problem:
  • Solution:
• 69. Sqrt(x)
  • Problem:
  • Solution:
• 71. Simplify Path
  • Problem:
  • Solution:
    • ONE
    • TWO
• 72. Edit Distance
  • Problem:
  • Solution:
• 73. Set Matrix Zeroes
  • Problem:
  • Solution:
    • ONE
    • TWO
• 74. Search a 2D Matrix
  • Problem:
  • Solution:
    • ONE
    • TWO
• 75. Sort Colors
  • Problem:
  • Solution:
• 77. Combinations
  • Problem:
  • Solution:
• 78. Subsets
  • Problem:
  • Solution:
    • ONE
    • TWO
• 79. Word Search
  • Problem:
  • Solution:
• 80. Remove Duplicates from Sorted Array II
  • Problem:
  • Solution:
• 81. Search in Rotated Sorted Array II
  • Problem:
  • Solution:
• 82. Remove Duplicates from Sorted List II
  • Problem:
  • Solution:
• 83. Remove Duplicates from Sorted List
  • Problem:
  • Solution:
    • ONE
    • TWO
• 84. Largest Rectangle in Histogram
  • Problem:
  • Solution:
• 85. Maximal Rectangle
  • Problem:
  • Solution:
    • ONE
    • TWO
• 86. Partition List
  • Problem:
  • Solution:
• 88. Merge Sorted Array
  • Problem:
  • Solution:
• 89. Gray Code
  • Problem:
  • Solution:
• 90. Subsets II
  • Problem:
  • Solution:
• 91. Decode Ways
  • Problem:
  • Solution:
• 92. Reverse Linked List II
  • Problem:
  • Solution:
• 93. Restore IP Addresses
  • Problem:
  • Solution:
• 97. Interleaving String
  • Problem:
  • Solution:
• 100. Same Tree
  • Problem:
  • Solution:
• 101. Symmetric Tree
  • Problem:
  • Solution:
    • ONE
    • TWO
• 102. Binary Tree Level Order Traversal
  • Problem:
  • Solution:
• 103. Binary Tree Zigzag Level Order Traversal
  • Problem:
  • Solution:
• 104. Maximum Depth of Binary Tree
  • Problem:
  • Solution:
• 105. Construct Binary Tree from Preorder and Inorder Traversal
  • Problem:
  • Solution:
• 106. Construct Binary Tree from Inorder and Postorder Traversal
  • Problem:
  • Solution:
• 107. Binary Tree Level Order Traversal II
  • Problem:
  • Solution:
• 110. Balanced Binary Tree
  • Problem:
  • Solution:
• 111. Minimum Depth of Binary Tree
  • Problem:
  • Solution:
• 112. Path Sum
  • Problem:
  • Solution:
• 113. Path Sum II
  • Problem:
  • Solution:
• 114. Flatten Binary Tree to Linked List
  • Problem:
  • Solution:
• 115. Distinct Subsequences
  • Problem:
  • Solution:
• 116. Populating Next Right Pointers in Each Node
  • Problem:
  • Solution:
    • ONE
    • TWO
• 117. Populating Next Right Pointers in Each Node II
  • Problem:
  • Solution:
    • ONE
    • TWO
• 118. Pascal’s Triangle
  • Problem:
  • Solution:
• 119. Pascal’s Triangle II
  • Problem:
  • Solution:
• 120. Triangle
  • Problem:
  • Solution:
• 121. Best Time to Buy and Sell Stock
  • Problem:
  • Solution:
• 122. Best Time to Buy and Sell Stock II
  • Problem:
  • Solution:
• 123. Best Time to Buy and Sell Stock III
  • Problem:
  • Solution:
• 124. Binary Tree Maximum Path Sum
  • Problem:
  • Solution:
    • ONE
    • TWO
• 125. Valid Palindrome
  • Problem:
  • Solution:
    • ONE
    • TWO
    • THREE
• 126. Word Ladder II
  • Problem:
  • Solution:
• 127. Word Ladder
  • Problem:
  • Solution:
• 128. Longest Consecutive Sequence
  • Problem:
  • Solution:
• 129. Sum Root to Leaf Numbers
  • Problem:
  • Solution:
• 130. Surrounded Regions
  • Problem:
  • Solution:
• 133. Clone Graph
  • Problem:
  • Solution:
• Balanced Binary Tree - LeetCode

≡